K
3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
SG
3
18 tháng 4 2017
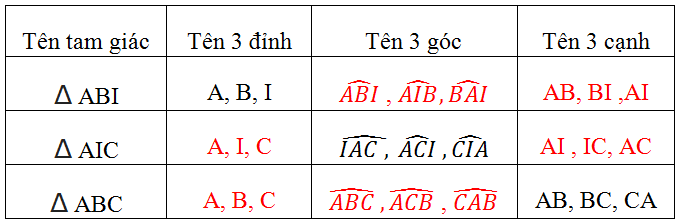
Giải:
|
Tên tam giác |
Tên 3 đỉnh |
Tên 3 góc |
Tên 3 cạnh |
|
|
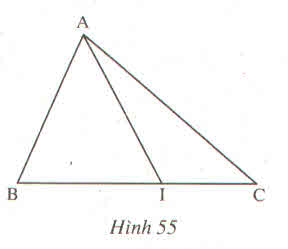
A,B,I |
|
AB, BI, IA |
|
|
A,I,C |
|
AI, IC, CA |
|
|
A,B,C |
|
AB, BC, CA |
SG
1
18 tháng 4 2017
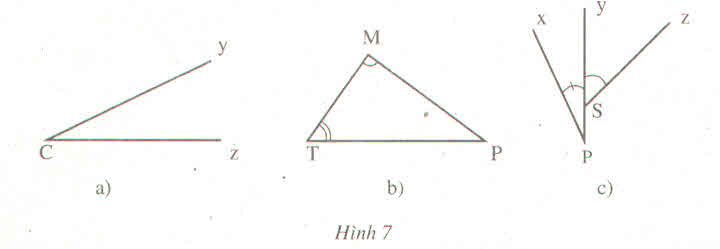
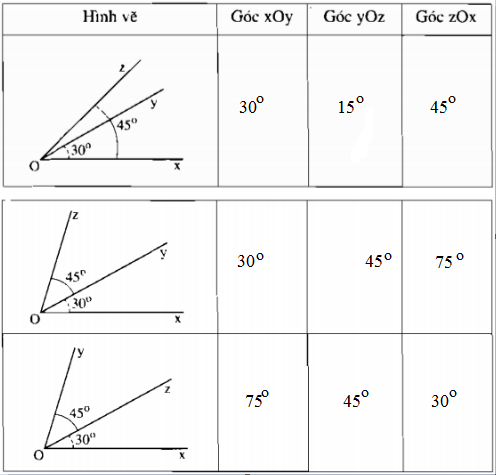
Giải:
|
Hình |
Tên góc (cách viết thông thường) |
Tên đỉnh |
Tên cạnh |
Tên góc (Cách viết kí hiệu) |
|
a |
Góc yCz, góc zCy, góc C |
C |
Cy,Cz |
|
|
b |
Góc MTP, PTM, T Góc TMP, PMT,M Góc TPM, MPT,P |
T M P |
TM,TP MT,MP PT,PM |
|
|
c |
Góc xPy,yPx,P Góc ySz,zSy |
P S |
Px, Py Sy, Sz |
|
13 tháng 5 2017
Bài giải:
|
Câu |
Đúng |
Sai |
|
a) 134 . 4 + 16 chia hết cho 4.
|
x |
|
|
b) 21 . 8 + 17 chia hết cho 8.
|
|
x |
|
c) 3 .100 + 34 chia hết cho 6.
|
|
x |
CC
4
27 tháng 8
Câu 8:
a:Sửa đề: \(4+4^2+\cdots+4^{2025}\)
Ta có: \(4+4^2+\cdots+4^{2025}\)
\(=\left(4+4^2+4^3\right)+\left(4^4+4^5+4^6\right)+\cdots+\left(4^{2023}+4^{2024}+4^{2025}\right)\)
\(=4\left(1+4+4^2\right)+4^4\left(1+4+4^2\right)+\cdots+4^{2023}\left(1+4+4^2\right)\)
\(=21\left(4+4^4+\cdots+4^{2023}\right)\) ⋮21
b: \(5+5^2+5^3+5^4+\cdots+5^{2024}\)
\(=\left(5+5^2\right)+\left(5^3+5^4\right)+\cdots+\left(5^{2023}+5^{2024}\right)\)
\(=\left(5+5^2\right)+5^2\left(5+5^2\right)+\cdots+5^{2022}\left(5+5^2\right)\)
\(=30\left(1+5^2+\cdots+5^{2022}\right)\) ⋮30
Câu 7:
a: \(A=2+2^2+2^3+\cdots+2^{99}\)
=>\(2A=2^2+2^3+\cdots+2^{100}\)
=>\(2A-A=2^2+2^3+\cdots+2^{100}-2-2^2-\cdots-2^{99}\)
=>\(A=2^{100}-2\)
b: \(B=1-7+7^2-7^3+\cdots+7^{48}-7^{49}\)
=>\(7B=7-7^2+7^3-7^4+\cdots+7^{49}-7^{50}\)
=>\(7B+B=7-7^2+7^3-7^4+\cdots+7^{49}-7^{50}+1-7+7^2-7^3+\cdots+7^{48}-7^{49}\)
=>\(8B=-7^{50}+1\)
=>\(B=\frac{-7^{50}+1}{8}\)
A
27 tháng 8
Câu 7
a) \(A=2+2^2+2^3+\ldots+2^{99}\).
Đây là cấp số nhân từ \(2^{1}\) đến \(2^{99}\). Tổng:
\(A = \sum_{k = 1}^{99} 2^{k} = \frac{2 \left(\right. 2^{99} - 1 \left.\right)}{2 - 1} = 2 \left(\right. 2^{99} - 1 \left.\right) = 2^{100} - 2.\)
b) \(B=1-7+7^2-7^3+\ldots+7^{48}-7^{49}\).
Đây là tổng các \(7^{k}\) với dấu luân phiên, tức là tổng cấp số nhân với tỉ số \(r = - 7\), từ \(k = 0\) đến \(k = 49\):
\(B = \sum_{k = 0}^{49} \left(\right. - 1 \left.\right)^{k} 7^{k} = \sum_{k = 0}^{49} \left(\right. - 7 \left.\right)^{k} = \frac{1 - \left(\right. - 7 \left.\right)^{50}}{1 - \left(\right. - 7 \left.\right)} = \frac{1 - 7^{50}}{8} .\)
(Đó là dạng rút gọn chính xác.)
Câu 8
a) Dạng đề: \(1+4+4^2+4^3+\ldots+4^{2025}\) chia hết cho \(21\) ?
Hãy xét chu kỳ của \(4^{n}\) theo mod \(21\). Ta có
\(4^{1} \equiv 4 , 4^{2} \equiv 16 , 4^{3} = 64 \equiv 1 \left(\right. m o d 21 \left.\right) ,\)
vậy \(4^{3} \equiv 1 \left(\right. m o d 21 \left.\right)\) — nghĩa là dãy lũy thừa của 4 theo mod 21 có chu kỳ 3. Tổng mỗi nhóm ba số liên tiếp
\(4^{0} + 4^{1} + 4^{2} = 1 + 4 + 16 = 21 \equiv 0 \left(\right. m o d 21 \left.\right) .\)
Tập các số từ \(4^{0}\) đến \(4^{2025}\) có \(2026\) số. Vì \(2026 = 3 \cdot 675 + 1\), nên ta có \(675\) nhóm 3 (mỗi nhóm tổng chia hết cho 21) và dư một số là \(4^{2025}\). Do \(2025\) chia hết cho \(3\), ta có \(4^{2025} \equiv 4^{0} \equiv 1 \left(\right. m o d 21 \left.\right)\).
Vậy tổng toàn bộ hợp lại
\(\equiv 675 \cdot 0 + 1 \equiv 1 \left(\right. m o d 21 \left.\right) ,\)
không chia hết cho \(21\).
Kết luận: Như đề bài viết (tới \(4^{2025}\)), tổng không chia hết cho \(21\).
(Có lẽ đề thực tế muốn mũ cuối là \(2024\) thay vì \(2025\); khi mũ cuối là \(2024\) thì có \(2025\) số, tức \(2025 = 3 \cdot 675\) nhóm đầy đủ nên tổng sẽ chia hết cho \(21\).)
b) Dạng đề: \(5 + 5^{2} + 5^{3} + \hdots + 5^{2024}\) chia hết cho \(30\) ?
Gọi \(S = \sum_{k = 1}^{2024} 5^{k}\). Ta kiểm tra chia hết cho \(2 , 3 , 5\) (vì \(30 = 2 \cdot 3 \cdot 5\)):
- Chia cho \(5\): mỗi \(5^{k}\) có \(5\) là thừa số, nên tổng \(S\) chia hết cho \(5\).
- Chia cho \(2\): với modulo \(2\), \(5 \equiv 1\). Do đó mỗi \(5^{k} \equiv 1 \left(\right. m o d 2 \left.\right)\). Có \(2024\) số nên tổng theo modulo \(2\) là \(2024 \cdot 1 \equiv 0 \left(\right. m o d 2 \left.\right)\). Vậy chia hết cho \(2\).
- Chia cho \(3\): \(5 \equiv 2 \left(\right. m o d 3 \left.\right)\). Lũy thừa luân phiên: \(5^{1} \equiv 2 , \textrm{ }\textrm{ } 5^{2} \equiv 1 , \textrm{ }\textrm{ } 5^{3} \equiv 2 , \textrm{ }\textrm{ } 5^{4} \equiv 1 , \ldots\) (chu kỳ 2). Vì \(2024\) là số chẵn, các cặp \(\left(\right. 5^{2 m - 1} + 5^{2 m} \left.\right) \equiv 2 + 1 \equiv 0 \left(\right. m o d 3 \left.\right)\). Do đó tổng chia hết cho \(3\).
Từ đó \(S\) chia hết cho \(2 , 3 , 5\) đồng thời, nên chia hết cho \(30\).
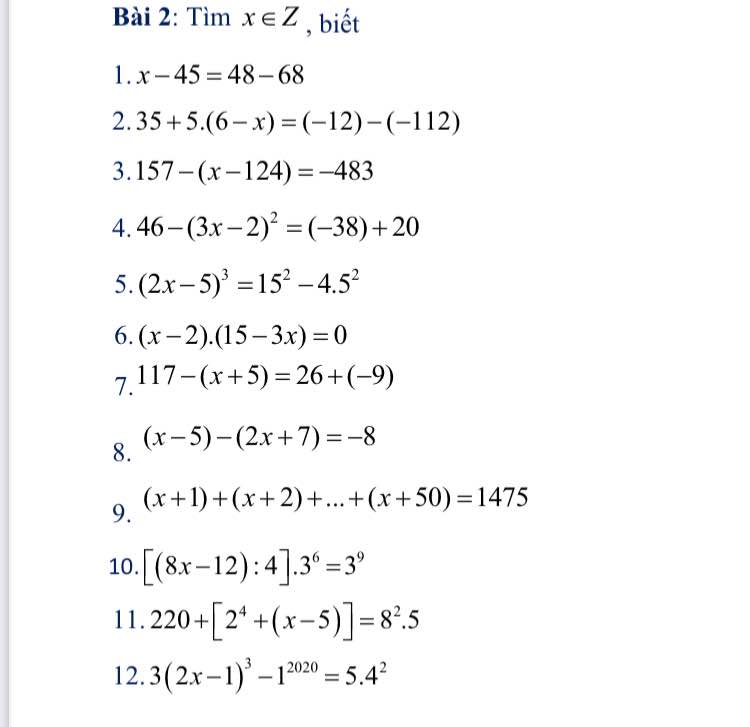
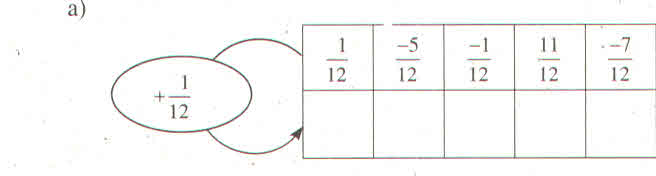
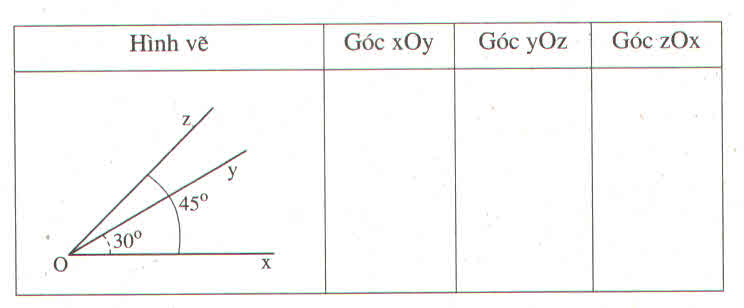
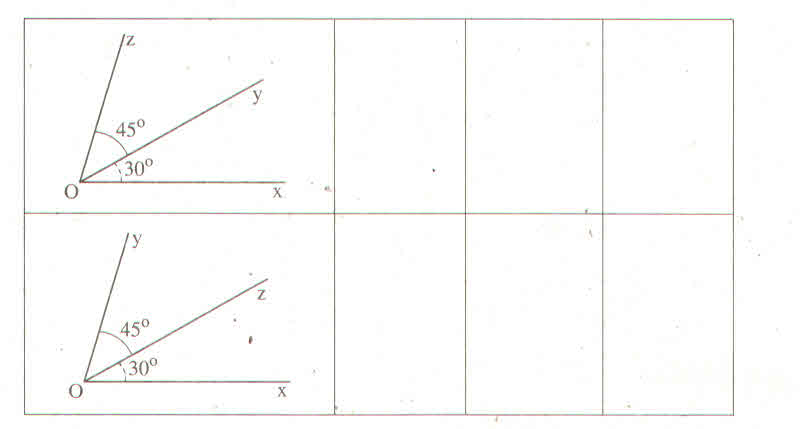
\(\left(x-5\right)-\left(2x+7\right)=-8\\ x-5-2x-7+8=0\\ -x=4\\ x=-4\)
Tách nhỏ câu hỏi ra bạn