KC
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
22 tháng 12 2022
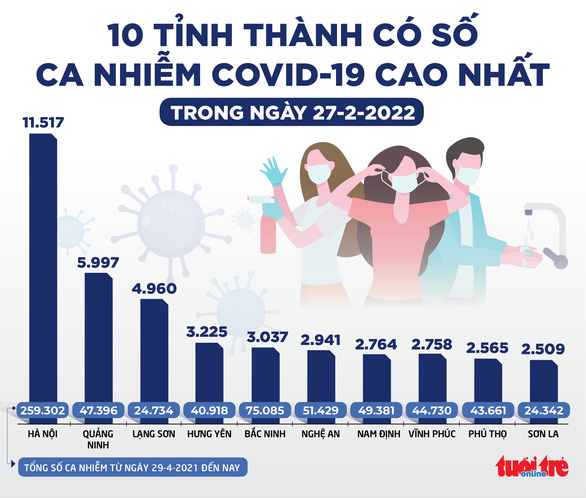
a. Những tỉnh thành phố có ca nhiễm hơn 2800 ca: Nghệ An, Bắc Ninh, Hưng Yên, Lạng Sơn, Quảng Ninh, Hà Nội.
b. Tỉnh có số ca nhiễm Covid 19 cao nhất là: Hà Nội
BM
1
10 tháng 8
F(x)⋮G(x)
=>\(2x^3-7x^2+12x+a\) ⋮x+2
=>\(2x^3+4x^2-11x^2-22x+34x+68+a-68\) ⋮x+2
=>a-68=0
=>a=68
KV
25 tháng 1 2024
\(5x=3y\Rightarrow x=\dfrac{3y}{5}\)
Thay \(x=\dfrac{3y}{5}\) vào biểu thức \(x^2-y^2=-4\) ta có:
\(\left(\dfrac{3y}{5}\right)^2-y^2=-4\)
\(\dfrac{9y^2}{25}-y^2=-4\)
\(-\dfrac{16}{25}y^2=-4\)
\(y^2=-\dfrac{4}{\dfrac{-16}{25}}\)
\(y^2=\dfrac{25}{4}\)
\(\Rightarrow y=-\dfrac{5}{2};y=\dfrac{5}{2}\)
*) \(y=-\dfrac{5}{2}\Rightarrow x=\dfrac{3.\left(-\dfrac{5}{2}\right)}{5}=-\dfrac{3}{2}\)
*) \(y=\dfrac{5}{2}\Rightarrow x=\dfrac{3.\dfrac{5}{2}}{5}=\dfrac{3}{2}\)
Vậy ta được các cặp giá trị \(\left(x;y\right)\) thỏa mãn:
\(\left(-\dfrac{3}{2};-\dfrac{5}{2}\right);\left(\dfrac{3}{2};\dfrac{5}{2}\right)\)
AH
Akai Haruma
Giáo viên
31 tháng 1 2024
Lời giải:
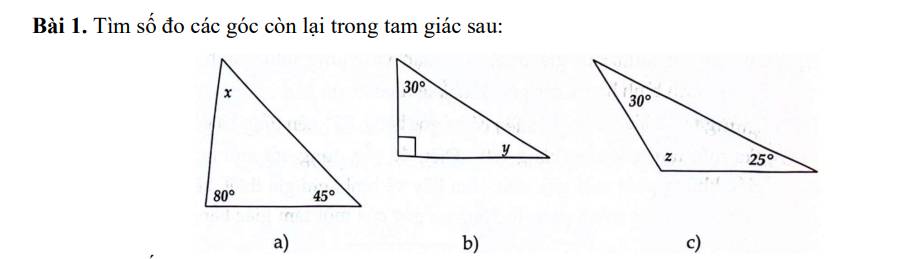
Áp dụng tính chất tổng 3 góc trong một tam giác bằng $180^0$
a.
$x=180^0-80^0-45^0=55^0$
b.
$y=180^0-30^0-90^0=60^0$
c.
$z=180^0-30^0-25^0=125^0$
10 tháng 8
a: \(5x\left(x-3\right)-x\left(5x+1\right)=16\)
=>\(5x^2-15x-5x^2-x=16\)
=>-16x=16
=>x=-1
b: \(4x\left(x-1\right)+x\left(3-4x\right)=5\)
=>\(4x^2-4x+3x-4x^2=5\)
=>-x=5
=>x=-5
c: \(5\left(x^2+4x-3\right)-x\left(5x+3\right)=19\)
=>\(5x^2+20x-15-5x^2-3x=19\)
=>17x=19+15=34
=>x=2
10 tháng 8
a: Thể tích của bể cá là: \(100\cdot60\cdot50=3000\cdot100=300000\left(\operatorname{cm}^3\right)\)
b: Thể tích nước ban đầu trong bể là:
\(100\cdot60\cdot30=6000\cdot30=180000\left(\operatorname{cm}^3\right)\)
\(30dm^3=30000\left(\operatorname{cm}^3\right)\)
Thể tích nước sau khi cho thêm hòn đá vào là:
\(180000+30000=210000\left(\operatorname{cm}^3\right)\)
Chiều cao của mực nước là:
210000:100:60=35(cm)
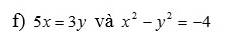
a.
\(A\in Z\Rightarrow2A\in Z\Rightarrow\dfrac{2\left(3x-2\right)}{2x-3}\in Z\)
\(\Rightarrow\dfrac{6x-4}{2x-3}\in Z\Rightarrow\dfrac{3\left(2x-3\right)+5}{2x-3}\in Z\)
\(\Rightarrow3+\dfrac{5}{2x-3}\in Z\Rightarrow\dfrac{5}{2x-3}\in Z\)
\(\Rightarrow2x-3=Ư\left(5\right)=\left\{-5;-1;1;5\right\}\)
\(\Rightarrow x=\left\{-1;1;2;4\right\}\)
Thử lại thấy đều thỏa mãn
b.
\(\dfrac{2x+4}{y}-\dfrac{2}{x}-\dfrac{5}{xy}=1\)
\(\Rightarrow x\left(2x+4\right)-2y-5=xy\)
\(\Leftrightarrow2x^2+4x-y-5=xy\)
\(\Leftrightarrow2x^2+4x-5=y\left(x+1\right)\)
Với \(x=-1\) không thỏa mãn
Với \(x\ne-1\Rightarrow y=\dfrac{2x^2+4x-5}{x+1}\) (1)
Do \(y\in Z\Rightarrow\dfrac{2x^2+4x-5}{x+1}\in Z\Rightarrow\dfrac{2x^2+4x+2-7}{x+1}\in Z\)
\(\Rightarrow\dfrac{2\left(x+1\right)^2-7}{x+1}\in Z\Rightarrow2\left(x+1\right)-\dfrac{7}{x+1}\in Z\)
\(\Rightarrow\dfrac{7}{x+1}\in Z\) do \(2\left(x+1\right)\in Z\) với \(x\in Z\)
\(\Rightarrow x+1=Ư\left(7\right)=\left\{-7;-1;1;7\right\}\)
\(\Rightarrow\left[{}\begin{matrix}x=-8\left(loại\right)\\x=-2\left(loại\right)\\x=0\\x=6\end{matrix}\right.\)
Thế vào (1): \(\left[{}\begin{matrix}x=0\Rightarrow y=-5< 0\left(loại\right)\\x=6\Rightarrow y=13\end{matrix}\right.\)
Vậy \(\left(x;y\right)=\left(6;13\right)\)