Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Diện tích mặt đáy của hình chóp tứ giác đều ABCD là: 30.30=900 (cm2)
- Thể tích hình chóp là:
\(V = \frac{1}{3}.S.h = \frac{1}{3}.900.30 = 9000(c{m^3})\)
- Thể tích hình lập phương là V=30.30.30=27000 (cm3)
Vậy thể tích phần gỗ bị cắt đi là V = 27000 − 9000=18000 (cm3)

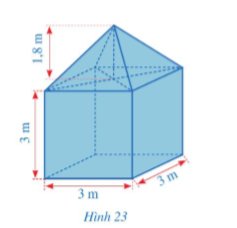
Thể tích của lều trại đó là.
\(V = {3^3} + \dfrac{1}{3}{3^2}.1,8 = 32,4({m^3})\)
Một khối gỗ gồm đế là hình lập phương cạnh 9 cm và một hình chóp tứ giác đều. Tính thể tích khối gỗ.
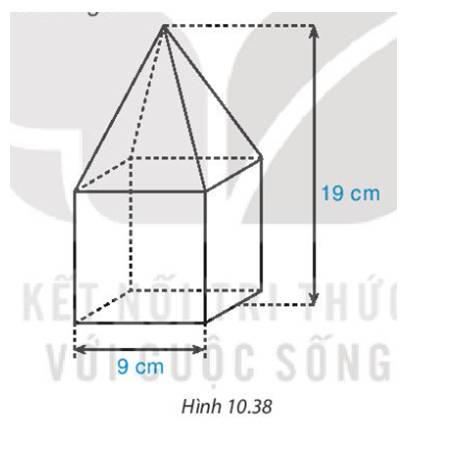

Có chiều cao của cả khối gỗ là 9 cm, chiều cao cụa hình lập phương là 9 cm
=> Chiều cao của hình chóp tứ giác đều là: 19−9=10 (cm)
- Diện tích mặt đáy của hình chóp tứ giác đều là: 9.9=81 (cm2)
- Thể tích hình chóp là:
\(V = \frac{1}{3}.S.h = \frac{1}{3}.81.10 = 270\left( {c{m^3}} \right)\)
- Thể tích hình lập phương là: V=9.9.9=729 \(\left( {c{m^3}} \right)\)
Vậy thể tích của khối gỗ là: 270+729= 999 (cm3)

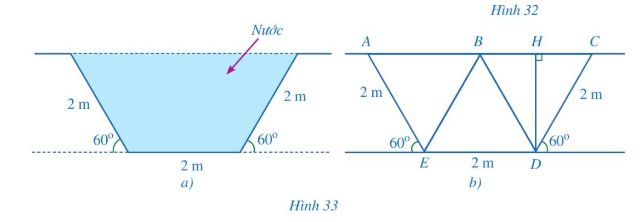
a, Do ACDE là hình thang cân nên
AC//DE suy ra AB//ED \( \Rightarrow {{\widehat B} _1} = {{\widehat E} _3},{{\widehat A} _1} = {{\widehat E} _1} = {60^0};{{\widehat C} _1} = {{\widehat D} _1} = {60^0}\)
Mà: AE//BD \( \Rightarrow {{\widehat B} _2} = {{\widehat E} _2}\)
Xét \(\Delta ABE\) và \(\Delta B{\rm{D}}E\) có: \({{\widehat B} _1} = {{\widehat E} _3}\) ; BE chung
\(\begin{array}{l}{{{\widehat B} }_2} = {{{\widehat E} }_2} \Rightarrow \Delta ABE = \Delta B{\rm{D}}E \Rightarrow A{\rm{E}} = B{\rm{D}} = 2m.\\AB = E{\rm{D}} = 2m\end{array}\)
Xét \(\Delta BC{\rm{D}}\) có \({{\widehat C} _1} = {60^0};B{\rm{D}} = C{\rm{D}} = 2m \Rightarrow \Delta BC{\rm{D}}\) đều.
Xét \(\Delta A{\rm{E}}B\) có \({{\widehat A} _1} = {60^0};AB = A{\rm{E}} = 2m \Rightarrow \Delta A{\rm{E}}B\) đều.
Vì: \(\Delta A{\rm{E}}B\) đều suy ra: BE = 2 m.
Xét \(\Delta BE{\rm{D}}\) có BD = BE = ED = 2m \( \Rightarrow \Delta BE{\rm{D}}\) đều.
b, Vì \(\Delta ABE,\Delta BC{\rm{D}}\) là các tam giác đều nên AB = BC = 2m.
Suy ra AC = AB + BC = 4m.
Do \(\Delta B{\rm{D}}C\) đều nên H là trung điểm của BC.
Suy ra HC = HB =\(\dfrac{{BC}}{2} = 1\)
Xét \(\Delta DHC\) vuông tại H ta có:
\(D{C^2} = D{H^2} + H{C^2}\) (theo định lý pythagore)
\(\begin{array}{l} \Rightarrow D{H^2} = D{C^2} - H{C^2} = {2^2} - {1^2} = 3\\ \Rightarrow DH = \sqrt 3 \end{array}\)
c, Diện tích hình thang cân AEDC là:
\({S_{A{\rm{ED}}C}} = \dfrac{1}{2}DH.(AC + E{\rm{D}}) = \dfrac{1}{2}\sqrt 3 (2 + 4) = 3\sqrt 3 (c{m^2})\)
Vậy diện tích mặt cắt phần chứa nước: \(3\sqrt 3 c{m^2}\)

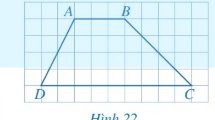
Hai cạnh AB và CD của tứ giác ABCD có song song với nhau.

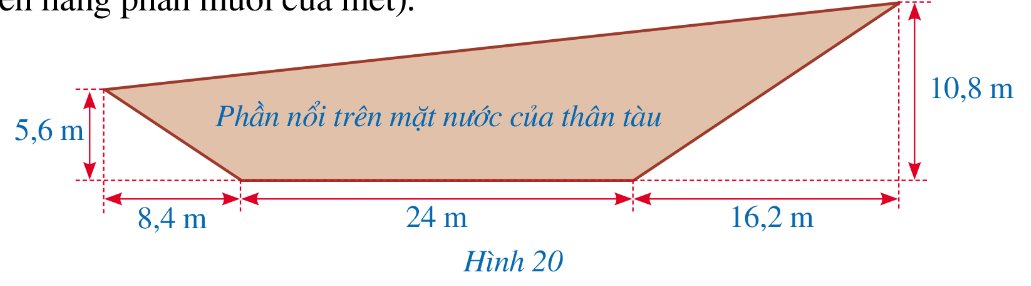
*) Áp dụng định lí Pythagore trong tam giác \(\Delta ABC\) vuông tại A có
\(A{C^2} = A{B^2} + B{C^2} = 5,{6^2} + 8,{4^2} = 101,92 \Rightarrow AC = \sqrt {101,92} \)
\(\Delta DEF\) vuông tại F có
\(D{F^2} = D{E^2} + E{F^2} = 16,{2^2} + 10,{8^2} = 379,08 \Rightarrow DF = \sqrt {379,08} \)
Kẻ \(AG \bot FG\)
Khi đó: \(FG = FE - GE = FE - AB = 10,8 - 5,6 = 5,2\)
Áp dụng định lí Pythagore trong \(\Delta AGF\) vuông tại G có
\(A{F^2} = A{G^2} + F{G^2} = 48,{6^2} + 5,{2^2} = 2389 \Rightarrow AF = \sqrt {2389} \)
Chu vi tứ giác ACDF là:
\(AC + CD + DF + AF = \sqrt {101,92} + \sqrt {379,08} + 24 + \sqrt {2389} \approx 102,4\)
Vậy chu vi của mặt cắt dọc phần nổi trên mặt nước của chiếc tàu thủy là khoảng 102,4m.

Áp dụng định lí Py-ta-go, ta có:
\(2,1^2+h^2=3,5^2\\ \Leftrightarrow h=\sqrt{3,5^2-2,1^2}=2,8m\)

Những hình khối có dạng ở hình 11 được gọi là hình chóp tứ giác đều.
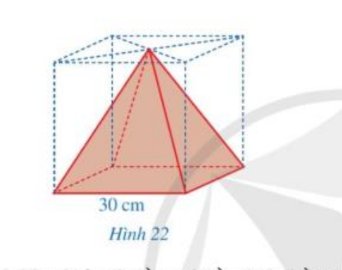
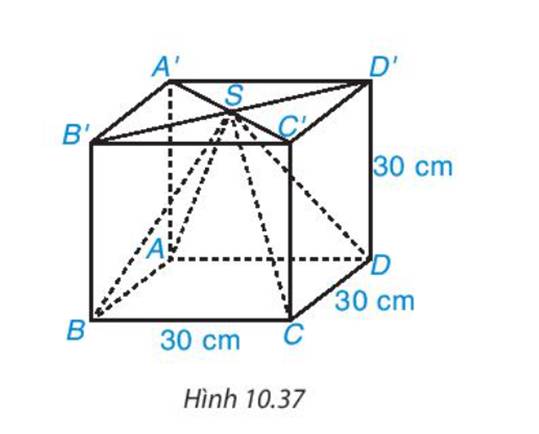



Thể tích của khối gỗ hình lập phương là:
\( V_{lp} = 30^3 = 27000 (cm^3)\)
Thể tích vật thể có hình chóp tứ giác đều là:
\(V_{hc} = \frac{1}{3}.30^2.30 = 9000 (cm^3)\)
Thể tích phần khúc gỗ bị cắt bỏ là:
\( V = V_{lp} - V_{hc} = 27000 - 9000 = 18000 (cm^3)\)
Vậy thể tích của phần khúc gỗ đã bị cắt bỏ là \(18000 cm^3\)