K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
1P
2
DH
Đỗ Hoàn
CTVHS
VIP
3 giờ trước (20:52)
+) Thales thuận: song song -> tỉ lệ
+) Hệ quả (Thales đảo): tỉ lệ -> song song
MN
Minh Ngọc Nguyễn
VIP
3 giờ trước (20:53)
So sánh:
- Định lý Thales: Điều kiện là đường thẳng song song ⇒ Kết luận các đoạn tỉ lệ.
- Hệ quả Thales (đảo): Điều kiện là các đoạn tỉ lệ ⇒ Kết luận đường thẳng song song.
Nói cách khác:
- Định lý: Song song → tỉ lệ
- Hệ quả: Tỉ lệ → song song
9 tháng 5 2022
Refer
Hệ quả của định lí Ta-lét
Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh tam giác đã cho.
10 tháng 9
1. Định lý Thalès (thuận)
Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại, thì nó định ra hai đoạn thẳng tỉ lệ trên hai cạnh đó.
Ví dụ:
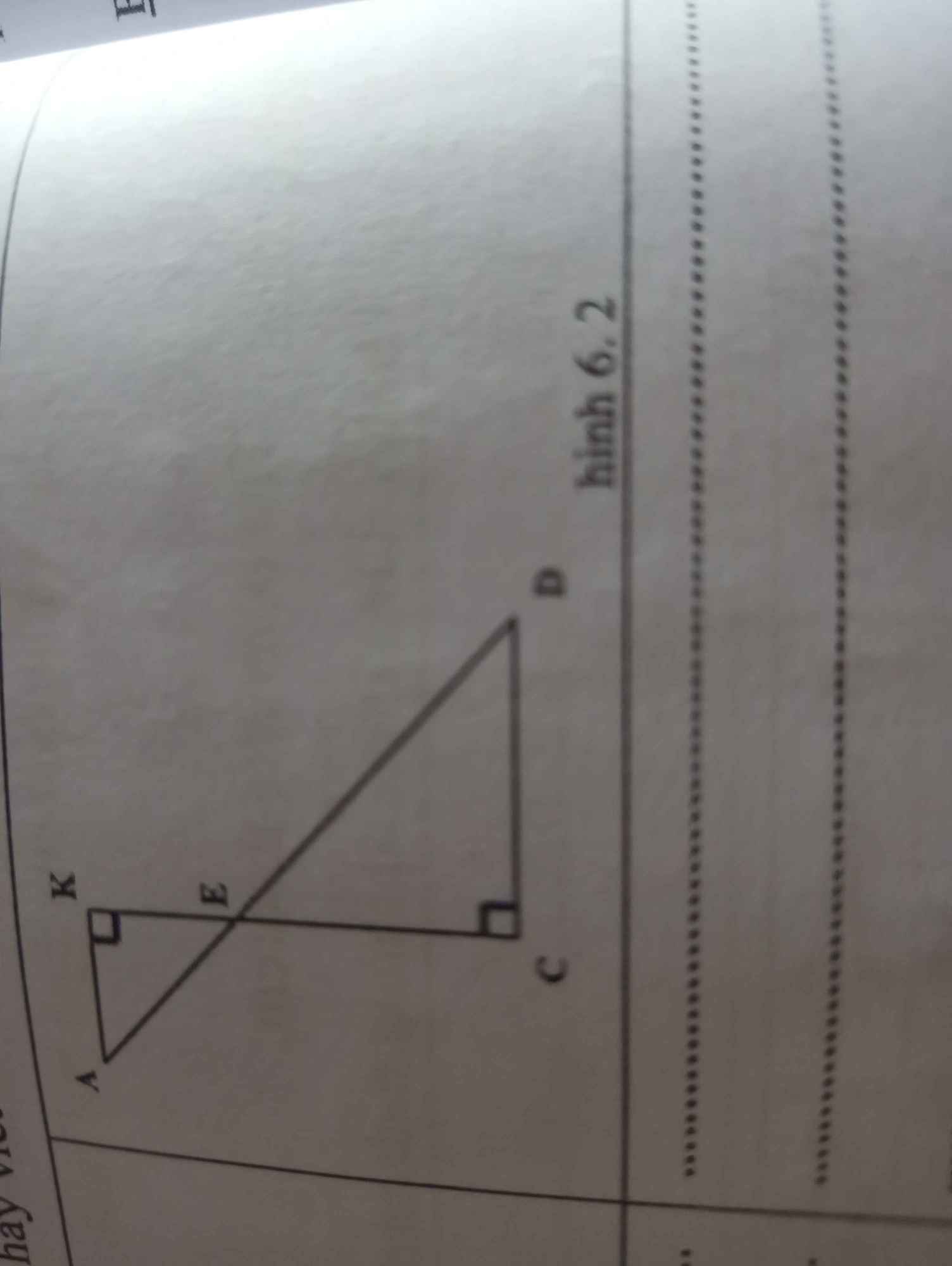
Trong tam giác \(A B C\), kẻ đường thẳng \(D E \parallel B C\), cắt \(A B\) tại \(D\), \(A C\) tại \(E\).
Ta có:
\(\frac{A D}{D B} = \frac{A E}{E C}\)
2. Hệ quả của định lý Thalès
Nếu một đường thẳng cắt hai cạnh của một tam giác và chia hai cạnh đó thành những đoạn tương ứng tỉ lệ, thì đường thẳng đó song song với cạnh còn lại của tam giác.
Ví dụ:
Trong tam giác \(A B C\), gọi \(D \in A B\), \(E \in A C\).
Nếu:
\(\frac{A D}{D B} = \frac{A E}{E C}\)
thì ta suy ra:
\(D E \parallel B C\)
👉 Nói ngắn gọn:
- Định lý Thalès thuận: song song → tỉ số bằng nhau.
- Hệ quả (Thalès đảo): tỉ số bằng nhau → song song.
23 tháng 12 2023
a: Xét ΔABC có
MN//BC
nên \(\dfrac{AM}{MB}=\dfrac{AN}{NC}\)
=>\(\dfrac{AN}{NC}=1\)
=>AN=NC
b: Xét tứ giác AICK có
N là trung điểm chung của AC và KI
=>AICK là hình bình hành
c: Xét ΔABC có AI là phân giác
nên \(\dfrac{IB}{IC}=\dfrac{AB}{AC}\)
\(\dfrac{MB}{NC}=\dfrac{AB}{2}:\dfrac{AC}{2}=\dfrac{AB}{AC}\)
=>\(\dfrac{IB}{IC}=\dfrac{MB}{NC}\)
=>\(IB\cdot NC=MB\cdot IC\)
BT
1
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 1 2024
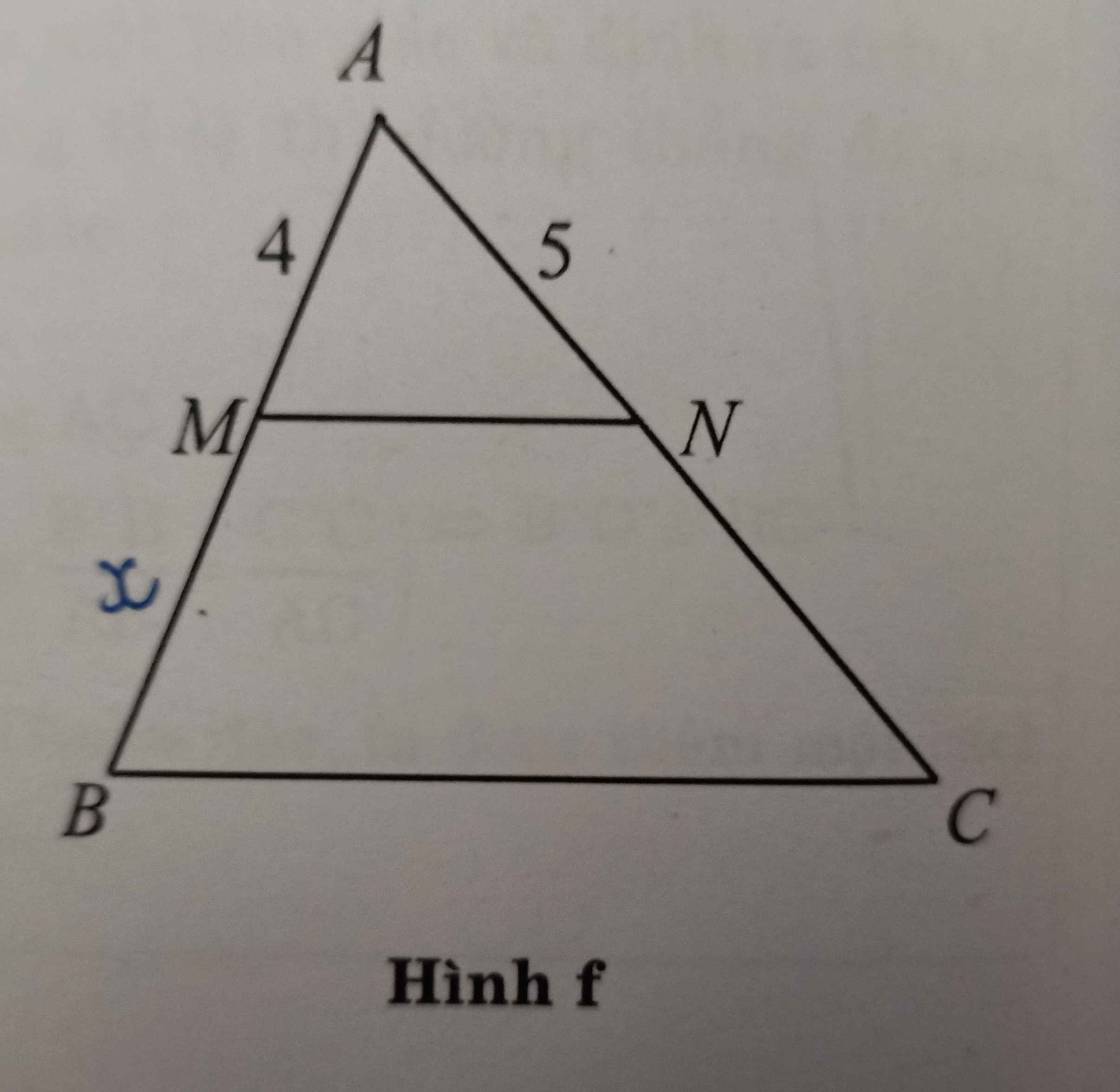
Hình f đề bài thiếu nên không tính được
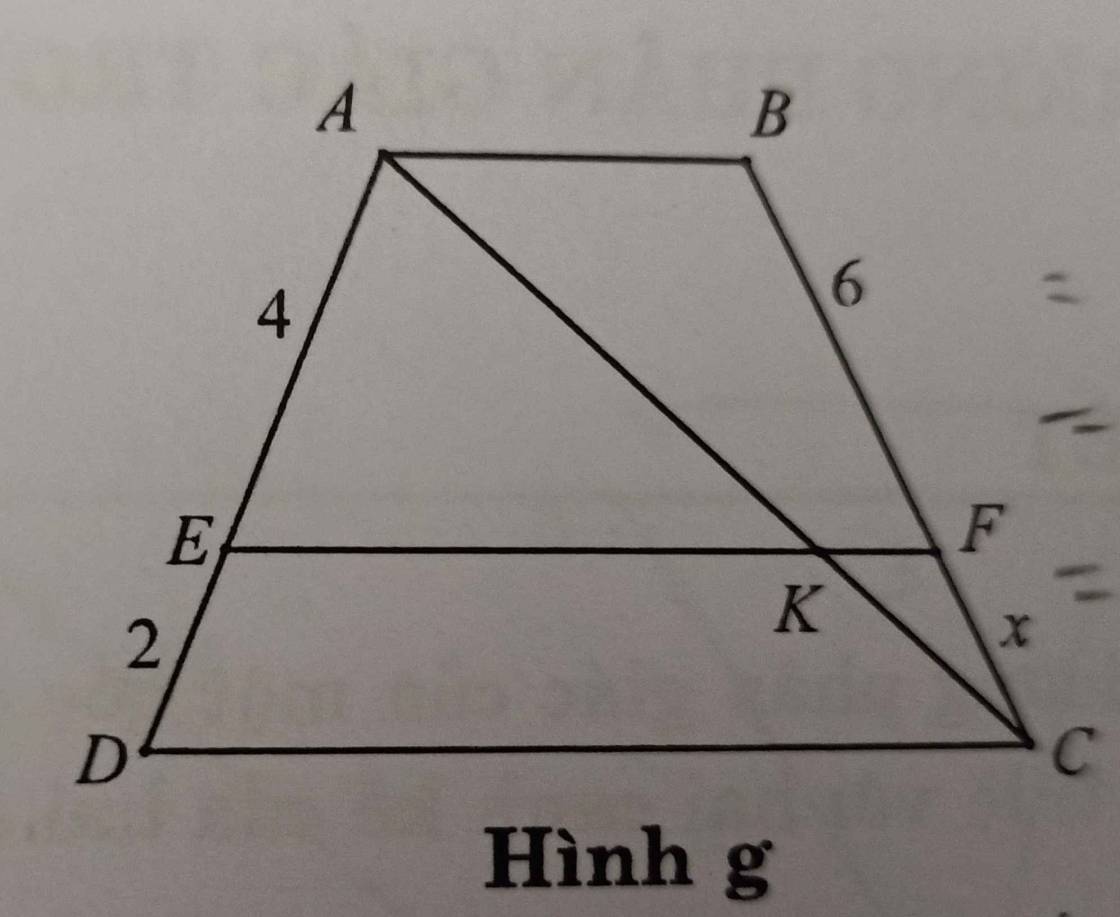
Với hình g:
Áp dụng định lý Talet cho tam giác ADC:
\(\dfrac{AE}{ED}=\dfrac{AK}{KC}\Rightarrow\dfrac{AK}{KC}=\dfrac{4}{2}=2\)
\(\Rightarrow\dfrac{CK}{AK}=\dfrac{1}{2}\)
Áp dụng định lý Talet cho tam giác CAB:
\(\dfrac{CF}{BF}=\dfrac{CK}{AK}\Rightarrow\dfrac{x}{6}=\dfrac{1}{2}\Rightarrow x=3\)
XO
22 tháng 7 2021
ĐK : 2x - 1 \(\ge0\)=> \(x\ge\frac{1}{2}\)
Khi đó |2x - 1| = 2x - 1
<=> \(\orbr{\begin{cases}2x-1=2x-1\\2x-1=-2x+1\end{cases}}\Leftrightarrow\orbr{\begin{cases}0x=0\\4x=2\end{cases}}\Leftrightarrow\orbr{\begin{cases}\forall x\\x=\frac{1}{2}\end{cases}}\Leftrightarrow\forall x\)
Kết hợp điều kiện => \(x\ge\frac{1}{2}\)là giá trị phải tìm
Vậy \(x\ge\frac{1}{2}\)là nghiệm phương trình
=> Chọn B
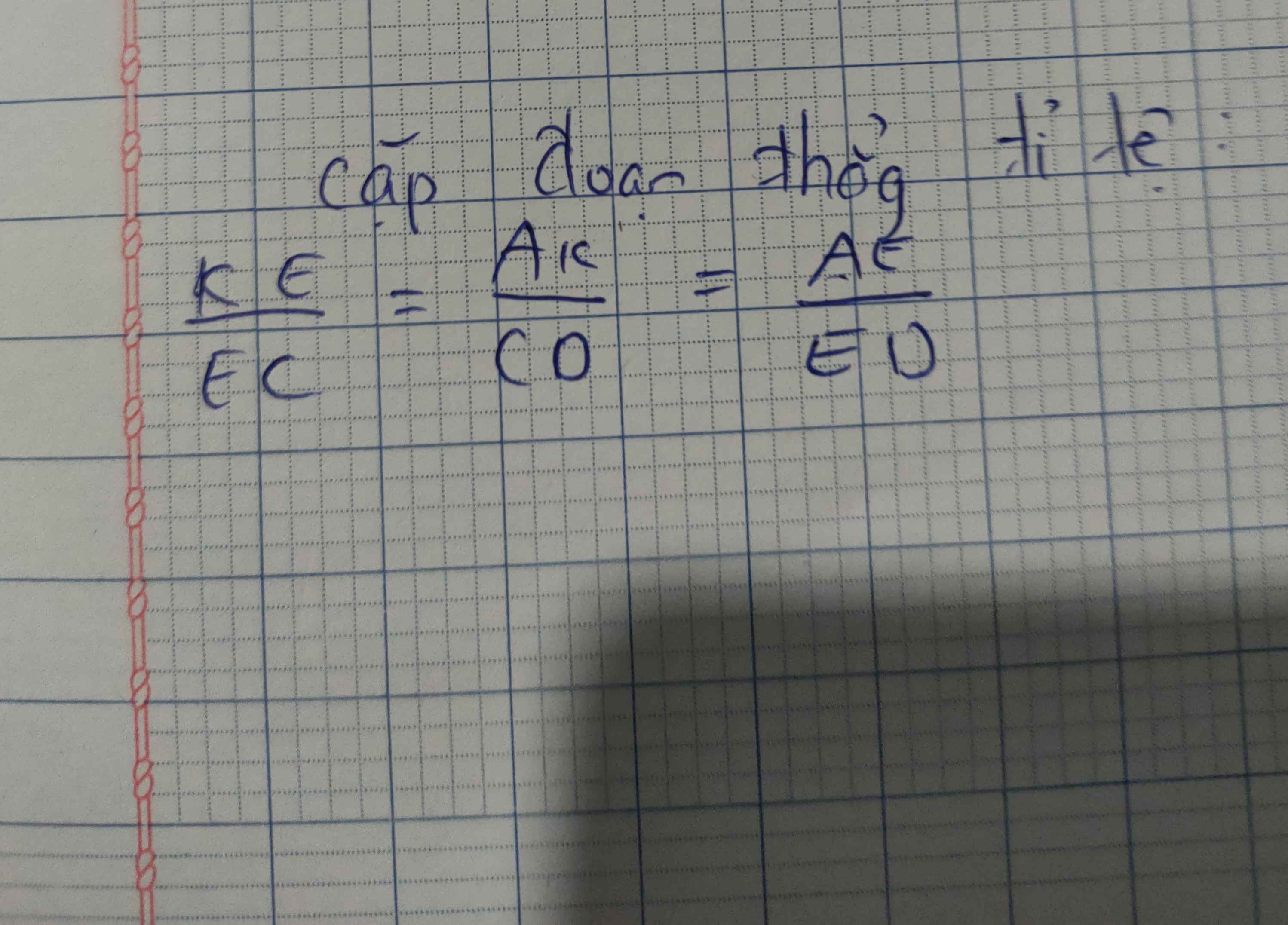
Thales là gì vậy bạn?