QT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
QT
1
HQ
Hà Quang Minh
Giáo viên
18 tháng 9 2023
Xét 2 tam giác ABC và MNP có:
AB=MN (gt)
\(\widehat {BAC} = \widehat {NMP}\) (gt)
AC=MP (gt)
Vậy \(\Delta ABC = \Delta MNP\)(c.g.c)
QT
1
HQ
Hà Quang Minh
Giáo viên
18 tháng 9 2023
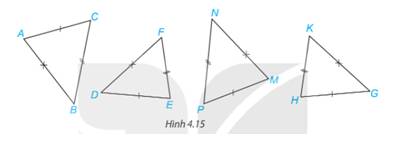
Xét \(\Delta ABC\) và \(\Delta MNP\) có:
\(\begin{array}{l}AB = MN\\BC = NP\\AC = MP\end{array}\)
Vậy\(\Delta ABC\) =\(\Delta MNP\)(c.c.c)
Xét \(\Delta DEF\) và \(\Delta GHK\) có:
\(\begin{array}{l}DE = GH\\EF = HK\\DF = GK\end{array}\)
Vậy\(\Delta DEF\)=\(\Delta GHK\) (c.c.c)
QT
1
18 tháng 9 2023
Em thấy bạn Vuông nói đúng
Để chứng minh điều này, ta có thể chỉ ra trường hợp 2 góc bằng nhau nhưng không đối đỉnh.
Ví dụ:
\(\widehat {{O_1}} = \widehat {{O_2}}\) nhưng hai góc này không đối đỉnh
QT
1
HQ
Hà Quang Minh
Giáo viên
18 tháng 9 2023
2 góc kề bù trong hình là: góc mOt và tOn
Ta có:
\(\begin{array}{l}\widehat {mOt} + \widehat {tOn} = 180^\circ \\\widehat {mOt} = 180^\circ - \widehat {tOn} = 180^\circ - 60^\circ = 120^\circ \end{array}\)
QT
1
HQ
Hà Quang Minh
Giáo viên
18 tháng 9 2023
Đoạn thẳng đơn vị được chia thành 6 phần bằng nhau, lấy một đoạn làm đơn vị mới, đơn vị mới bằng \(\frac{1}{6}\) đơn vị cũ.
Điểm A nằm bên phải gốc O và cách O một đoạn bằng 10 đơn vị mới. Do đó điểm A biểu diễn số hữu tỉ \(\frac{{10}}{6} = \frac{5}{3}\)
Điểm B nằm bên trái gốc O và cách O một đoạn bằng 5 đơn vị mới. Do đó điểm B biểu diễn số hữu tỉ \(\frac{{ - 5}}{6}\)
Điểm C nằm bên trái gốc O và cách O một đoạn bằng 13 đơn vị mới. Do đó điểm C biểu diễn số hữu tỉ \(\frac{{ - 13}}{6}\)
QT
1
19 tháng 9
d: \(\frac27-\left(\frac23+2x\right)=\frac57\)
=>\(2x+\frac23=\frac27-\frac57=-\frac37\)
=>\(2x=-\frac37-\frac23=-\frac{9}{21}-\frac{14}{21}=-\frac{23}{21}\)
=>\(x=-\frac{23}{21}:2=-\frac{23}{42}\)
e: \(\frac12-2x=\left(-\frac12\right)^3\)
=>\(\frac12-2x=-\frac18\)
=>\(2x=\frac12+\frac18=\frac58\)
=>\(x=\frac58:2=\frac{5}{16}\)
f: \(\left(2x-3\right)\left(\frac34x+1\right)=0\)
=>\(\left[\begin{array}{l}2x-3=0\\ \frac34x+1=0\end{array}\right.\Rightarrow\left[\begin{array}{l}2x=3\\ \frac34x=-1\end{array}\right.\Rightarrow\left[\begin{array}{l}x=\frac32\\ x=-\frac43\end{array}\right.\)
g: \(\frac{7}{12}-\left(x+\frac76\right):\frac65=-\frac54\)
=>\(\left(x+\frac76\right):\frac65=\frac{7}{12}+\frac54=\frac{7}{12}+\frac{15}{12}=\frac{22}{12}=\frac{11}{6}\)
=>\(x+\frac76=\frac{11}{6}\cdot\frac65=\frac{11}{5}\)
=>\(x=\frac{11}{5}-\frac76=\frac{66}{30}-\frac{35}{30}=\frac{31}{30}\)
h: \(\frac34:\left(x+\frac12\right)-\frac56=-\frac14\)
=>\(\frac34:\left(x+\frac12\right)=-\frac14+\frac56=-\frac{3}{12}+\frac{10}{12}=\frac{7}{12}\)
=>\(x+\frac12=\frac34:\frac{7}{12}=\frac34\cdot\frac{12}{7}=\frac{36}{28}=\frac97\)
=>\(x=\frac97-\frac12=\frac{18}{14}-\frac{7}{14}=\frac{11}{14}\)
i: \(\frac25x+\frac35x=\frac34\)
=>\(x\left(\frac25+\frac35\right)=\frac34\)
=>\(x\cdot\frac55=\frac34\)
=>\(x=\frac34\)
k: \(\frac12x+\frac23x-x=\frac13\)
=>\(x\left(\frac12+\frac23-1\right)=\frac13\)
=>\(x\left(\frac12-\frac13\right)=\frac13\)
=>\(x\cdot\frac16=\frac13\)
=>\(x=\frac13:\frac16=2\)
l: \(\left(\frac32-\frac{2}{-5}\right):x-\frac12=\frac32\)
=>\(\left(\frac32+\frac25\right):x=\frac32+\frac12=2\)
=>\(\left(\frac{15}{10}+\frac{4}{10}\right):x=2\)
=>\(\frac{19}{10}:x=2\)
=>\(x=\frac{19}{10}:2=\frac{19}{20}\)
m: \(\left(5x-1\right)\left(2x-\frac13\right)=0\)
=>\(\left[\begin{array}{l}5x-1=0\\ 2x-\frac13=0\end{array}\right.\Rightarrow\left[\begin{array}{l}5x=1\\ 2x=\frac13\end{array}\right.\Rightarrow\left[\begin{array}{l}x=\frac15\\ x=\frac16\end{array}\right.\)
HQ
Hà Quang Minh
Giáo viên
18 tháng 9 2023
Do hai tam giác trên có hai cặp góc bằng nhau nên cặp góc còn lại bằng nhau.
Xét \(\Delta ABC\) và \(\Delta A'B'C'\) có:
\(\widehat A = \widehat {A'}\) (gt)
AC = A'C' (gt)
\(\widehat C = \widehat {C'}\) (cmt)
\(\Rightarrow \Delta ABC = \Delta A'B'C'\) (g.c.g)
Vậy hai tam giác đã cho bằng nhau theo trường hợp góc – cạnh – góc.
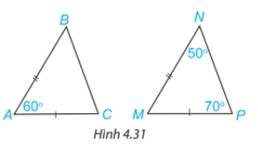
Xét tam giác MNP có:
\(\begin{array}{l}\widehat M + \widehat N + \widehat P = {180^o}\\ \Rightarrow \widehat M + {50^o} + {70^o} = {180^o}\\ \Rightarrow \widehat M = {60^o}\end{array}\)
Xét 2 tam giác ABC và MNP có:
AB=MN (gt)
\(\widehat {BAC} = \widehat {NMP} (=60^0)\)
AC=MP (gt)
Vậy \(\Delta ABC = \Delta MNP\)(c.g.c)