Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

10cm A H B O
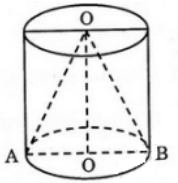
Giả sử căt hình đó thành 1 mặt phẳng đi qua trục của nón ta được thiết diện như hình vẽ. Trong đó tam giác ABC là tam giác đều và là thiết diện của khối nón. Hình tròn tâm I là thiết diện của quả bóng.
Ta nhận thấy tam giác ABC ngoại tiếp đường tròn tâm I
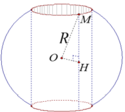
Hình nón có chiều cao là \(OH=3IH=30\) (cm)
Bán kính đáy nón là \(HA=\frac{30}{\sqrt{3}}=10\sqrt{3}\left(cm\right)\)
Thể tích khối nón là \(V_1=\frac{1}{3}OH.\pi.AH^2=\frac{1}{3}.30\pi.300=3000\pi\left(cm^3\right)\)
Thể tích phần không gian bên trong khối nón không bị quả bóng chiếm chỗ là :
\(V_2=\frac{1}{3}OH.\pi.AH^2-\frac{1}{4}\pi.IH^2=3000\pi-\frac{4000}{3}\pi=\frac{5000}{3}\pi\left(cm^3\right)\)














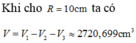
Bước 1: Tính thể tích của quả cầu toàn bộ.
Công thức tính thể tích của quả cầu là:
\(V = \frac{4}{3} \pi r^{3}\)
Với bán kính của quả cầu \(r = 10 \&\text{nbsp};\text{cm}\), ta thay vào công thức:
\(V = \frac{4}{3} \pi \left(\right. 10 \left.\right)^{3} = \frac{4}{3} \pi \times 1000 = \frac{4000}{3} \pi \approx 4188.79 \&\text{nbsp};\text{cm}^{3}\)
Bước 2: Tính thể tích của một phần quả cầu.
Quả cầu được cắt thành 8 phần đều nhau, do đó thể tích của một phần quả cầu sẽ là thể tích toàn bộ quả cầu chia cho 8:
\(V_{\text{m} \overset{\sim}{\hat{\text{o}}} \text{i}\&\text{nbsp};\text{ph} \overset{ˋ}{\hat{\text{a}}} \text{n}} = \frac{1}{8} \times V_{\text{to} \overset{ˋ}{\text{a}} \text{n}\&\text{nbsp};\text{b}ộ} = \frac{1}{8} \times \frac{4000}{3} \pi = \frac{500}{3} \pi \approx 523.60 \&\text{nbsp};\text{cm}^{3}\)
Kết luận: Thể tích của một phần quả cầu là 523.60 cm³.