Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án A
LCω2 = 2 → Lω = 2/Cω → ZL = 2ZC
(1): 
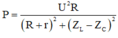
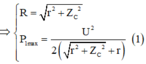
(2): 
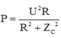
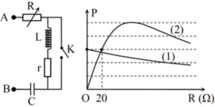
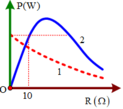
Từ đồ thị
(3)
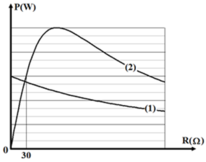
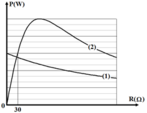
Khi R = 30 Ω → P2max = P1
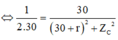(4)
Từ (3) và (4), suy ra r = 270 Ω
Đáp án A
Có
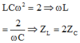
Theo đồ thị có:
- Đường (1): mạch RrLC :
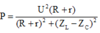
Dùng BĐT Cauchy dễ dàng tìm ra
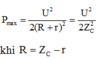
Để ý thấy đường (1) không có đỉnh cực đại
Lại có khi R = 0 thì P ứng với 9 dòng
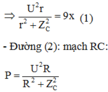
Dùng BĐT Cauchy tìm ra
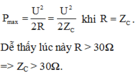
Theo đồ thị thấy Pmax ứng với 15 ô
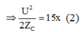
Lại có khi R = 30 Ω thì P ứng với 9 ô
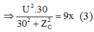
Từ (2) và (3)
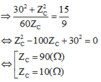
Vì Z C > 30 Ω nên chọn Z C = 90 Ω .
Từ (1) và (2) có:
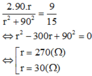
Vì r > Z C nên chọn r = 270 Ω
\(U_C=I.Z_C=\dfrac{U.Z_C}{\sqrt{R^2+(Z_L-Z_C)^2}}=\dfrac{U}{\sqrt{R^2+(\omega.L-\dfrac{1}{\omega C})^2}.\omega C}=\dfrac{U}{\sqrt{\omega^2.C^2.R^2+(\omega^2.LC-1)^2}}\)
Suy ra khi \(\omega=0\) thì \(U_C=U\) \(\Rightarrow (1)\) là \(U_C\)
\(U_L=I.Z_L=\dfrac{U.Z_L}{\sqrt{R^2+(Z_L-Z_C)^2}}=\dfrac{U.\omega L}{\sqrt{R^2+(\omega.L-\dfrac{1}{\omega C})^2}}=\dfrac{U.L}{\sqrt{\dfrac{R^2}{\omega^2}+(L-\dfrac{1}{\omega^2 C})^2}}\)(chia cả tử và mẫu cho \(\omega\))
Suy ra khi \(\omega\rightarrow \infty\) thì \(U_L\rightarrow U\) \(\Rightarrow (3) \) là \(U_L\)
Vậy chọn \(U_C,U_R,U_L\)
1. Cường độ dòng điện cùng pha với điện áp -> \(Z_L=Z_C\)
Nếu nối tắt tụ C thì mạch chỉ còn R nối tiếp với L.
\(\tan\varphi=\frac{Z_L}{R}=\tan\frac{\pi}{3}=\sqrt{3}\Rightarrow Z_L=\sqrt{3}.50=50\sqrt{3}\Omega\)
\(\Rightarrow Z_C=50\sqrt{3}\Omega\)
2. Cuộn dây phải có điện trở R
Ta có giản đồ véc tơ
Ud Uc Um 120 120 Ur 45 0
Từ giản đồ ta có: \(U_C=\sqrt{120^2+120^2}=120\sqrt{2}V\)
\(U_R=120\cos45^0=60\sqrt{2}V\)
Cường độ dòng điện: \(I=\frac{U_C}{Z_C}=\frac{120\sqrt{2}}{200}=0,6\sqrt{2}V\)
Công suất: \(P=I^2R=I.U_R=0,6\sqrt{2}.60\sqrt{2}=72W\)
Khi trong mạch xảy ra cộng hưởng thì ω = ${\omega _0} = \dfrac{1}{{\sqrt {LC} }}$.
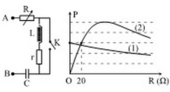
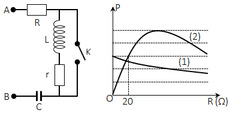
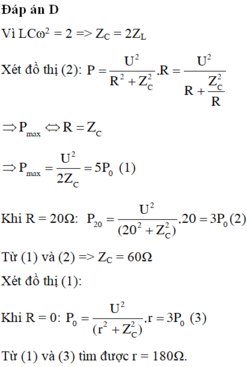
Đáp án A
Sử dụng “Kĩ thuật đồ thị”, kết hợp với các công thức về công suất, ta có
- Theo đề:
- Khi K mở:
- Khi K đóng:
Và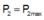
khi 
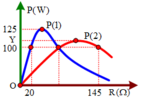
- Trên đồ thị, ta có:
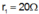- Khi
thì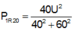 
mà theo đồ thị thì
nên loại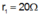
và chọn 