Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
3 vecto của 3 dao động tạo thành tam giác đều (vì cùng biên độ)
Pha ban đầu của dao động thứ 2 là: \(\phi=-\frac{\pi}{12}-\frac{\pi}{3}=-\frac{5\pi}{12}\left(rad\right)\)
Biên độ dao động tổng hợp thỏa mãn: \(\left|A_1-A_2\right|\le A\le\left|A_1+A_2\right|\)
\(\Rightarrow\) A = 5 (cm) thỏa mãn hệ thức
Đáp án D
Phương pháp: Sử dụng̣ giản đồ Fresnen
Cách giải:
x1 + x2 = x => x1 +6 = 9cm => x1 = 3cm
Dựa vào đề bài ta biểu diễn được các vecto dao động như hình bên:
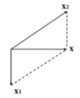
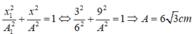
Áp dụng công thức (5.1 và 5.2 - SGK) ta tìm được:
A = 2,3 cm và φ = 0,73π
Phương trình dao động tổng hợp là: x = 2,3cos(5πt + 0,73π) (cm).
Đáp án C
Phương pháp: Công thức tính biên độ dao động tổng hợp hai dao động điều hòa cùng phương, cùng tần số
Cách giải:
Gọi A1, A2 là biên độ của hai dao động thành phần.
Nếu 2 dao động thành phần lệch pha
Nếu hai dao động thành phần ngược pha thì A 1 - A 2 = 15 , 6 c m (2)
Từ (1) và (2) => A1 = 19,6cm, A2 = 4cm.
Nếu 2 dao động thành phần cùng pha thì
=> Biên độ dao động tổng hợp là: A = A1 + A2 = 23,6cm
Hướng dẫn: Chọn đáp án C
⇒ 16 . 3 = 16 + A 2 2 - 2 . 4 . A 2 cos π 3
⇒ A 2 = 8 c m ⇒ C h ọ n C h o ặ c A 2 = - 4 c m
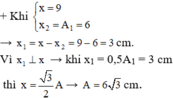
Đáp án B
Biên độ tổng hợp của hai dao động ngược pha: A = A 1 − A 2