Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giả sử \(A B C D\) là hình thang với \(A B \parallel C D\), hai cạnh đáy không bằng nhau \(\left(\right. A B \neq C D \left.\right)\) và hai cạnh bên bằng nhau \(\left(\right. A D = B C \left.\right)\).
Gọi \(E , F\) lần lượt là hình chiếu vuông góc của \(A\) và \(B\) xuống đường thẳng \(C D\).
- Vì \(A B \parallel C D\), khoảng cách giữa hai đường thẳng song song là không đổi nên \(A E = B F\) (cùng là “chiều cao” của hình thang).
- Xét hai tam giác vuông \(\triangle A E D\) và \(\triangle B F C\):
- \(A E = B F\) (lập luận trên),
- \(A D = B C\) (giả thiết),
- Cả hai đều vuông tại \(E\) và \(F\).
⇒ \(\triangle A E D \cong \triangle B F C\) (theo cạnh–góc vuông–cạnh, hay RHS).
Từ đó suy ra các góc nhọn ứng nhau bằng nhau:
\(\angle A D C = \angle E D A = \angle C F B = \angle D C B .\)
Vậy \(\angle D = \angle C\).
Do \(A B \parallel C D\) nên các cặp góc kề bù theo cùng phía tạo bởi cạnh bên thỏa:
\(\angle A + \angle D = 180^{\circ} , \angle B + \angle C = 180^{\circ} .\)
Mà \(\angle D = \angle C\) nên suy ra \(\angle A = \angle B\).
Kết luận: hình thang có hai cạnh đáy không bằng nhau và hai cạnh bên bằng nhau thì có hai góc kề mỗi đáy bằng nhau, nên là hình thang cân.
ASK CHATJPT
Gọi hình thang đề bài cho là ABCD với hai đáy là AB,CD
Gọi M là giao điểm của AD và BC
Xét ΔMDC có AB//DC
nên \(\frac{MA}{AD}=\frac{MB}{BC}\)
mà AD=BC
nên MA=MB
Ta có: MA+AD=MD
MB+BC=MC
mà MA=MB và AD=BC
nên MD=MC
=>ΔMDC cân tại M
=>\(\hat{MDC}=\hat{MCD}\)
=>\(\hat{ADC}=\hat{BCD}\)
Xét hình thang BADC(AB//CD) có \(\hat{ADC}=\hat{BCD}\)
nên BADC là hình thang cân

Câu |
Khẳng định |
Đúng |
Sai |
1 |
Hình thang là tứ giác có các cạnh đối song song |
x |
|
2 |
Hình thang có hai cạnh bên bằng nhau là hình thang cân |
|
x |
3 |
Hình bình hành là tứ giác có hai đường chéo bằng nhau |
|
x |
4 |
Hình thang có hai cạnh bên song song là hình bình hành |
x |
|

a) Đúng, vì hình thang có hai đáy song song lại có thêm hai cạnh đáy bằng nhau nên là hình bình hành theo dấu hiệu nhận biết 5
b) Đúng, vì khi đó ta được tứ giác có các cạnh đối song song là hình bình hành (định nghĩa)
c) Sai.
Ví dụ tứ giác ABCD ở dưới có AB = CD nhưng không phải hình bình hành.
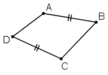
d) Sai, vì hình thang cân có hai cạnh bên bằng nhau nhưng nó không phải là hình bình hành.
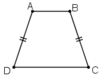

a) Đúng, vì hình thang có hai đáy song song lại có thêm hai cạnh đáy bàng nhau nên là hình bình hành theo dấu hiệu nhận biết 5.
b) Đúng, vì khi đó ta được tứ giác có các cạnh đối song song là hình bình hành (định nghĩa).
c) Sai, vì hình thang cân có hai cạnh đối (hai cạnh bên) bằng nhau nhưng nó không phải là hình bình hành.
d) Sai, vì hình thang cân có hai cạnh bên bằng nhau nhưng nó không phải là hình bình hành.
Bài giải:
a) Đúng, vì hình thang có hai đáy song song lại có thêm hai cạnh đáy bàng nhau nên là hình bình hành theo dấu hiệu nhận biết 5.
b) Đúng, vì khi đó ta được tứ giác có các cạnh đối song song là hình bình hành (định nghĩa).
c) Sai, vì hình thang cân có hai cạnh đối (hai cạnh bên) bằng nhau nhưng nó không phải là hình bình hành.
d) Sai, vì hình thang cân có hai cạnh bên bằng nhau nhưng nó không phải là hình bình hành.

+ Tứ giác có hai cạnh bên bằng nhau là hình thang cân.
→ Đáp án A sai vì hai cạnh bên bằng nhau chưa chắc tạo ra hình thang.
+ Hình thang cân có hai cạnh bên bằng nhau.
→ Đáp án B đúng.
+ Hình thang cân có hai góc kề một cạnh đáy bằng nhau.
→ Đáp án D đúng, đáp án C sai.

+ Tứ giác có hai cạnh bên bằng nhau là hình thang cân.
→ Đáp án A sai vì hai cạnh bên bằng nhau chưa chắc tạo ra hình thang.
+ Hình thang cân có hai cạnh bên bằng nhau.
→ Đáp án B đúng.
+ Hình thang cân có hai góc kề một cạnh đáy bằng nhau.
→ Đáp án D đúng, đáp án C sai.