Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Giải theo tiểu học vì bài này là chương trình lớp 5.
Giảm dài 2 lần mà tăng rộng 3 lần mà chu vi không đổi có nghĩa là phần tăng và giảm là bằng nhau.
giảm dài 2 lần tức là mất đi 1/2 chiều dài. Rộng tăng 3 lần có nghĩa là chiều rộng thêm 2 lần của nó nửa. Vậy 1/2 chiều dài bằng 2 lần chiều rộng hay chiều dài bằng 4 lần chiều rộng.
Giải theo dạng tìm hai số khi biết hiệu và tỷ của nó.
Chiều rộng là: 45:(4-1)x 1= 15m và chiều dài là 15+45=60m
Diện tích: 60x15= 900m2
Gọi chiều dài và chiều rộng của hình chữ nhật lần lượt là \(x,y\left(x>y>0\right)\)(đơn vị: m)
Vì chu vi của hình chữ nhật là 600m nên ta có phương trình \(2\left(x+y\right)=600\Leftrightarrow x+y=300\)(1)
Chiều dài lúc sau là: \(x-\frac{1}{5}x=\frac{4}{5}x\)(m)
Chiều rộng lúc sau là: \(y+\frac{3}{10}y=\frac{13}{10}y\)(m)
Vì chu vi của hình chữ nhật lúc sau là không đổi (vẫn là 600m) nên ta có phương trình \(2\left(\frac{4}{5}x+\frac{13}{10}y\right)=600\Leftrightarrow\frac{4}{5}x+\frac{13}{10}y=300\Leftrightarrow8x+13y=3000\)(2)
Từ (1) và (2) ta có hệ phương trình \(\hept{\begin{cases}x+y=300\\8x+13y=3000\end{cases}}\Leftrightarrow\hept{\begin{cases}8x+8y=2400\\8x+13y=3000\end{cases}}\Leftrightarrow\hept{\begin{cases}5y=600\\x+y=300\end{cases}}\Leftrightarrow\hept{\begin{cases}y=120\\x=180\end{cases}}\)(nhận)
Vậy chiều dài hình chữ nhật là 180m, chiều rộng là 120m.
Gọi chiều dài và chiều rộng lần lượt là \(x,y\left(m\right);x,y>0\).
Ta có hệ phương trình:
\(\hept{\begin{cases}2\left(x+y\right)=600\\2\left(\frac{4}{5}x+\frac{13}{10}y\right)=600\end{cases}}\Leftrightarrow\hept{\begin{cases}x+y=300\\8x+13y=3000\end{cases}}\Leftrightarrow\hept{\begin{cases}x=180\\y=120\end{cases}}\)(thỏa mãn)
Vậy chiều dài và chiều rộng của hình chữ nhật lần lượt là \(180m,120m\).
Bài 5: Gọi thời gian làm riêng của người thứ nhất và người thứ hai lần lượt là x(ngày) và y(ngày)
(Điều kiện: x>0; y>0)
Trong 1 ngày, người thứ nhất làm được: \(\frac{1}{x}\) (công việc)
Trong 1 ngày, người thứ hai làm được: \(\frac{1}{y}\) (công việc)
Trong 1 ngày, hai người làm được: \(\frac16\) (công việc)
Do đó, ta có: \(\frac{1}{x}+\frac{1}{y}=\frac16\left(1\right)\)
Trong 3 ngày, người thứ nhất làm được: \(\frac{3}{x}\) (công việc)
Trong 3+4=7 ngày, người thứ hai làm được: \(\frac{7}{y}\) (công việc)
Sau khi làm chung trong 3 ngày thì người thứ nhất đi làm việc khác, người thứ hai hoàn thành phần còn lại trong 4 ngày nên ta có: \(\frac{3}{x}+\frac{7}{y}=1\left(2\right)\)
Từ (1),(2) ta có hệ phương trình:
\(\begin{cases}\frac{1}{x}+\frac{1}{y}=\frac16\\ \frac{3}{x}+\frac{7}{y}=1\end{cases}\Rightarrow\begin{cases}\frac{3}{x}+\frac{3}{y}=\frac36=\frac12\\ \frac{3}{x}+\frac{7}{y}=1\end{cases}\)
=>\(\begin{cases}\frac{3}{x}+\frac{7}{y}-\frac{3}{x}-\frac{3}{y}=1-\frac12=\frac12\\ \frac{1}{x}+\frac{1}{y}=\frac16\end{cases}\Rightarrow\begin{cases}\frac{4}{y}=\frac12\\ \frac{1}{x}=\frac16-\frac{1}{y}\end{cases}\)
=>\(\begin{cases}y=8\\ \frac{1}{x}=\frac16-\frac18=\frac{1}{24}\end{cases}\Rightarrow\begin{cases}y=8\\ x=24\end{cases}\) (nhận)
Vậy: thời gian làm riêng của người thứ nhất và người thứ hai lần lượt là 24(ngày) và 8(ngày)
Bài 3:
Gọi số sản phẩm tổ 1 và tổ 2 làm được trong tháng thứ nhất lần lượt là x(sản phẩm) và y(sản phẩm)
(Điều kiện: x,y∈N*)
Tổng số sản phẩm hai tổ làm được trong tháng thứ nhất là 500 sản phẩm nên x+y=500(3)
Số sản phẩm tổ 1 làm được trong tháng thứ hai là: \(x\left(1+10\%\right)=1,1x\) (sản phẩm)
Số sản phẩm tổ 2 làm được trong tháng thứ hai là:
\(y\left(1+15\%\right)=1,15y\) (sản phẩm)
Tổng số sản phẩm hai tổ làm được trong tháng thứ hai là 564 sản phẩm nên 1,1x+1,15y=564(4)
Từ (3),(4) ta có hệ phương trình:
\(\begin{cases}x+y=500\\ 1,1x+1,15y=564\end{cases}\Rightarrow\begin{cases}1,1x+1,1y=550\\ 1,1x+1,15y=564\end{cases}\)
=>\(\begin{cases}1,1x+1,15y-1,1x-1,1y=564-550=14\\ x+y=500\end{cases}\)
=>\(\begin{cases}0,05y=14\\ x+y=500\end{cases}\Rightarrow\begin{cases}y=280\\ x=500-280=220\end{cases}\) (nhận)
Vậy: số sản phẩm tổ 1 và tổ 2 làm được trong tháng thứ nhất lần lượt là 220(sản phẩm) và 280(sản phẩm)
ặc. mình nhầm
nửa chu vi là: 250:2=125
gọi chiều dài là x (m;x>0)
chiều rộng là: 125-x(m)
=> chều dài thay đổi: x/3; chiều rộng thay đổi 2(125-x) (m)
vì chu vi k đổi nên ta có pt: \(\left(\frac{x}{3}+2\left(125-x\right)\right)2=250\Leftrightarrow\frac{-10}{3}x=-250\Leftrightarrow x=75\)( t/m đk)
=> dài: 75m. rộng: 125-75=50 m
gọi chiều dài là x (m;x>0)
chiều rộng là: 250-x(m)
=> chều dài thay đổi: x/3; chiều rộng thay đổi 2(250-x) (m)
chu vi: 250.2=500(m)
vì chu vi k đổi nên ta có pt: \(\frac{x}{3}+2\left(250-x\right)=500\Leftrightarrow\frac{-5}{3}x=0\Rightarrow x=0\)(k t/m đk)
=> k tìm đc x
Ta có:
π(2R)2 = 4πR2
π(3R)2 = 9 πR2
π(kR)2 = k2 πR2
Vậy nếu ta gấp đôi bán kính thì diện tích hình tròn sẽ gấp bốn, nếu nhân bán kính với k > 0 thì diện tích hình tròn sẽ gấp k2 lần
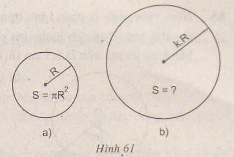
Ta có:
π(2R)2 = 4πR2
π(3R)2 = 9 πR2
π(kR)2 = k2 πR2
Vậy nếu ta gấp đôi bán kính thì diện tích hình tròn sẽ gấp bốn, nếu nhân bán kính với k > 0 thì diện tích hình tròn sẽ gấp k2 lần.
Tham khảo tại đây nha:
Câu hỏi của Moe - Toán lớp 9 - Học toán với online math
mã câu :1308090
ABCDEF12
a)Theo định lý Pi-ta-go , ta có :
BC2 = AB2 + AC2
BC2 = 62 + 82
BC2 = 100
=> BC = 10
\(sinB=\frac{AC}{BC}=\frac{8}{10}=\frac{4}{5}\)
\(\Rightarrow\widehat{B}\approx53^08^'\)
\(\Rightarrow\widehat{C}\approx90^0-\widehat{B}\approx90^0-53^08^'\approx36^052^'\)
b) AD là phân giác của \(\widehat{A}\)
\(\Rightarrow\widehat{A_1}=\widehat{A_2}=\frac{\widehat{A}}{2}=\frac{90^0}{2}=45^0\)
\(\frac{BD}{DC}=\frac{AB}{AC}=\frac{6}{8}=\frac{3}{4}\)
\(\Rightarrow\frac{BD}{3}=\frac{CD}{4}=\frac{CD+CD}{7}=\frac{10}{7}\)
\(\Rightarrow BD=\frac{3.10}{7}=\frac{30}{7}\)
\(\Rightarrow CD=\frac{4.10}{7}=\frac{40}{7}\)
c) Tứ giác AEDF có \(\widehat{A}=\widehat{F}=\widehat{E}=90^{^0}\)
=> AEDF là hình chữ nhật .
AD là phân giác của \(\widehat{A}\)
=> AEDF là hình vuông .
\(DE\perp AB\) \(AC\perp AB\) => DE // AC
\(\frac{CD}{BC}=\frac{AE}{AB}\) ( đl Ta lét )
=> \(AE=\frac{CD.AB}{BC}=\frac{\frac{40}{7}.6}{10}=\frac{24}{7}\)
Chu vi tứ giác AEDF = \(\frac{24}{7}.4=\frac{96}{7}\)
\(S_{AEDF}=\left(\frac{24}{7}\right)^2=\frac{576}{49}\left(cm\right)\)
Đáp án là D