Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
A B C D N M P K I
a) Gọi \(NP\cap CD=K\).
Do \(K\in NP\) nên \(K\in\left(MNP\right)\). Vậy K là giao điểm của CD và (MNP).
b) Do \(M\in AC\) nên \(M\in\left(MNP\right)\cap\left(ACD\right)\).
Và K là giao điểm của CD và (MNP) nên \(K\in\left(MNP\right)\cap\left(ACD\right)\).
Vì vậy MK là giao tuyến của (MNP) và (ACD).
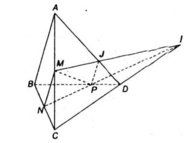
a) Ta có:
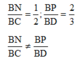
⇒ NP và CD không song song với nhau.
Gọi giao điểm NP và CD là I.
I ∈ NP ⇒ I ∈ (MNP).
Mà I ∈ CD
Vậy I ∈ CD ∩ (MNP)
b) Trong mặt phẳng (ACD) thì AD và MI cắt nhau tại điểm J:
J ∈ AD ⇒ J ∈ (ACD)
J ∈ MI ⇒ J ∈ (MNP)
Vậy J là một điểm chung của hai mặt phẳng (ACD) và (MNP).
Ta đã có M là một điểm chung của hai mặt phẳng (ACD) và (MNP).
Vậy MJ = (ACD) ∩ (MNP).
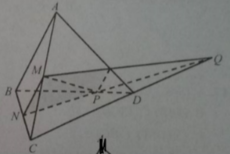
a) Ta có: MP cắt BC tại E mà BC thuộc (BCD)
Nên: E là giao điểm của đường thẳng MP với mặt phẳng (BCD).
b) Ta có: EN cắt CD tại Q mà EN thuộc (MNP)
Nên: Q là giao điểm của đường thẳng CD với mặt phẳng (MNP).
c) Ta có: P thuộc (MNP) và (ACD)
Q thuộc (MNP) và (ACD)
Nên PQ là giao tuyến của mặt phẳng (ACD) với mặt phẳng (MNP).
d) △ACN có: \(\dfrac{AP}{AC}=\dfrac{AG}{AN}=\dfrac{2}{3}\)
Suy ra: PG // CN
Do đó: △PIG đồng dạng với △NIC
Do đó: C, I, G thẳng hàng.
*Giao tuyến của (MNP) và (ABC)
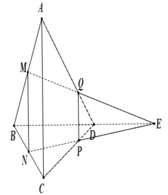
Trong mp(ABC), gọi E là giao điểm của MP và AC
E∈MP⊂(MNP)
E∈AC⊂(ABC)
Do đó: E∈(MNP) giao (ABC)(1)
P∈AB⊂(ABC)
P∈(MNP)
Do đó: P∈(ABC) giao (MNP)(2)
Từ (1),(2) suy ra (MNP) giao (ABC)=EP
*Giao tuyến của (MNP) và (ADC)
N∈DC⊂(ACD)
N∈(MNP)
Do đó: N∈(ACD) giao (MNP)(3)
E∈AC⊂(ACD)
E∈MP⊂(MNP)
Do đó: E∈(ACD) giao (MNP)(4)
Từ (3),(4) suy ra (ACD) giao (MNP)=NE
*Giao tuyến của (MNP) và (ABD)
Xét ΔCBD có
M,N lần lượt là trung điểm của CB,CD
=>MN là đường trung bình của ΔCBD
=>MN//BD
Xét (MNP) và (ABD) có
P∈(MNP) giao (ABD)
MN//BD
Do đó: (MNP) giao (ABD)=xy, xy đi qua P và xy//MN
*Giao tuyến của (MNP) và (BCD)
M∈BC⊂(BCD)
M∈(MNP)
Do đó; M∈(BCD) giao (MNP)(5)
N∈CD⊂(BCD)
N∈(MNP)
Do đó: N∈(BCD) giao (MNP)(6)
Từ (5),(6) suy ra (BCD) giao (MNP)=MN
Đáp án A
Gọi 
thì Q là giao điểm của (MNP) và AD.
Áp dụng định lí Menelaus trong ∆ B C D ta có:
Áp dụng định lí Menelaus trong ∆ ABD ta có:
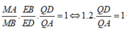
Áp dụng định lí Mê-nê-la-uýt:
Đáp án A