Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét tam giác DEH và tam giác DFH ta có:
DE = DF ( tam giác DEF cân tại D )
DEH = DFH ( tam giác DEF cân tại D )
EH = EF ( H là trung điểm của EF )
=> tam giác DEH = tam giác DFH ( c.g.c) (dpcm)
=> DHE=DHF(hai góc tương ứng)
Mà DHE+DHF=180 độ =>DHE=DHF=180 độ / 2 = 90 độ ( góc vuông ) hay DH vuông góc với EF ( dpcm )
b) Xét tam giác MEH và tam giac NFH ta có:
EH=FH(theo a)
MEH=NFH(theo a)
=> tam giác MEH = tam giác NFH ( ch-gn)
=> HM=HN ( 2 cạnh tương ứng ) hay tam giác HMN cân tại H ( dpcm )
c) Ta có : +) DM+ME=DE =>DM=DE-ME
+) DN+NF=DF => DN=DF-NF
Mà DE=DF(theo a) ; ME=NF( theo b tam giác MEH=tam giác NFH)
=>DM=DN => tam giác DMN cân tại D
Xét tam giac cân DMN ta có:
DMN=DNM=180-MDN/2 (*)
Xét tam giác cân DEF ta có:
DEF=DFE =180-MDN/2 (*)
Từ (*) và (*) Suy ra góc DMN = góc DEF
Mà DMN và DEF ở vị trí đồng vị
=> MN//EF (dpcm)
d) Xét tam giác DEK và tam giác DFK ta có:
DK là cạnh chung
DE=DF(theo a)
=> tam giác DEK= tam giác DFK(ch-cgv)
=>DKE=DKF(2 góc tương ứng)
=>DK là tia phân giác của góc EDF (1)
Theo a tam giac DEH= tam giac DFH(c.g.c)
=>EDH=FDH(2 góc tương ứng)
=>DH là tia phân giác của góc EDF (2)
Từ (1) và (2) Suy ra D,H,K thẳng hàng (dpcm)

a)Xét\(\Delta DEF\)có:\(EF^2=DE^2+DF^2\)(Định lý Py-ta-go)
hay\(5^2=3^2+DF^2\)
\(\Rightarrow DF^2=5^2-3^2=25-9=16\)
\(\Rightarrow DF=\sqrt{16}=4\left(cm\right)\)
Ta có:\(DE=3cm\)
\(DF=4cm\)
\(EF=5cm\)
\(\Rightarrow DE< DF< EF\)hay\(3< 4< 5\)
b)Xét\(\Delta DEF\)và\(\Delta DKF\)có:
\(DE=DK\)(\(D\)là trung điểm của\(EK\))
\(\widehat{EDF}=\widehat{KDF}\left(=90^o\right)\)
\(DF\)là cạnh chung
Do đó:\(\Delta DEF=\Delta DKF\)(c-g-c)
\(\Rightarrow EF=KF\)(2 cạnh t/ứ)
Xét\(\Delta KEF\)có:\(EF=KF\left(cmt\right)\)
Do đó:\(\Delta KEF\)cân tại\(F\)(Định nghĩa\(\Delta\)cân)
c)Ta có:\(DF\)cắt\(EK\)tại\(D\)là trung điểm của\(EK\Rightarrow DF\)là đg trung tuyến xuất phát từ đỉnh\(F\)của\(\Delta KEF\)
\(KI\)cắt\(EF\)tại\(I\)là trung điểm của\(EF\Rightarrow KI\)là đg trung tuyến xuất phát từ đỉnh\(K\)của\(\Delta KEF\)
Ta lại có:\(DF\)cắt\(KI\)tại\(G\)
mà\(DF\)là đg trung tuyến xuất phát từ đỉnh\(F\)của\(\Delta KEF\)
\(KI\)là đg trung tuyến xuất phát từ đỉnh\(K\)của\(\Delta KEF\)
\(\Rightarrow G\)là trọng tâm của\(\Delta KEF\)
\(\Rightarrow GF=\frac{2}{3}DF\)(Định lí về TC của 3 đg trung tuyến của 1\(\Delta\))
\(=\frac{2}{3}.4=\frac{8}{3}\approx2,7\left(cm\right)\)
Vậy\(GF\approx2,7cm\)

a) Áp dụng định lí Pytago vào ΔDEF vuông tại D, ta được:
\(EF^2=DE^2+DF^2\)
\(\Leftrightarrow EF^2=9^2+12^2=225\)
hay EF=15(cm)
Vậy: EF=15cm

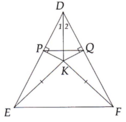
a, Ta có: DK là đường cao trong tam giác cân DEF
⇒DK vừa là đường cao, vừa là đường trung tuyến trong tam giác cân
⇒KE=KF
Ta có: KE=KF=EF/2=8/2=4 (cm)
Xét Δ vuông DKF
Theo định lý Pi-ta-go, ta có:
DF²=DK²+KF²
⇒DK²=DF²-KF²
⇒DK²=5²-4²
⇒DK²=9