Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét \(\Delta ABK\),ta có: BE là phân giác \(\angle ABK,BE\bot AK\)
\(\Rightarrow\Delta ABK\) cân tại B \(\Rightarrow BE\) là trung trực AK
Xét \(\Delta ABD\) và \(\Delta KBD:\) Ta có: \(\left\{{}\begin{matrix}AB=BK\\BDchung\\\angle ABD=\angle KBD\end{matrix}\right.\)
\(\Rightarrow\Delta ABD\sim\Delta KBD\left(c-g-c\right)\Rightarrow\angle BKD=\angle BAD=90\)
Ta có: \(\angle BAD+\angle BKD=90+90=180\Rightarrow BAKD\) nội tiếp
\(\Rightarrow\angle AKD=\angle ABD=\angle KBD=\angle KAH\left(=90-\angle BKA\right)\)
\(\Rightarrow\)\(AI\parallel KD\)
Vì \(I\in BE\Rightarrow IA=IK\Rightarrow\Delta IAK\) cân tại I \(\Rightarrow\angle IKA=\angle IAK\)
BADK nội tiếp \(\Rightarrow\angle KAD=\angle KBD=\angle ABD=\angle AKD\)
\(\Rightarrow\angle IKA=\angle DAK\Rightarrow\)\(IK\parallel AD\Rightarrow AIKD\) là hình bình hành
mà \(IA=IK\Rightarrow IKDA\) là hình thoi

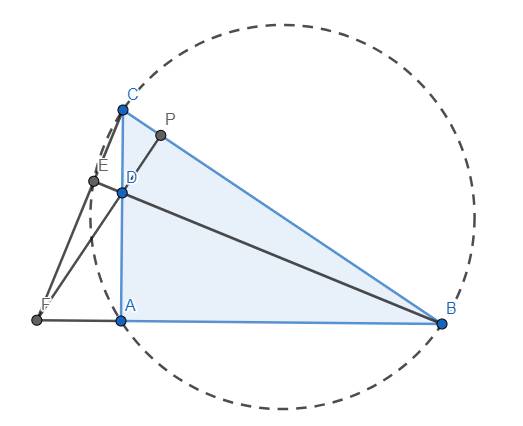
a) Ta có \(\widehat{CEB}=\widehat{CAB}=90^o\) nên 4 điểm A, B, C, E cùng thuộc đường tròn đường kính BC.
b) Kẻ \(FP\perp BC\) tại P. Ta thấy D là trực tâm tam giác FBC nên \(P\in DF\). Dễ thấy \(\Delta CDP~\Delta CBA\left(g.g\right)\) \(\Rightarrow\dfrac{CD}{CB}=\dfrac{CP}{CA}\) \(\Rightarrow CD.CA=CB.CP\)
CMTT, ta có \(BD.BE=BC.BP\)
Do đó \(CD.CA+BD.BE=CB.CP+BC.BP\) \(=BC\left(CP+BP\right)\) \(=BC^2\). Vậy đẳng thức được chứng minh.