

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




a) Tính số đo các góc BOD, DOE, COE
Dựa vào các số đo đã cho:
Giả sử các tia nằm trên cùng một mặt phẳng và theo thứ tự: B → O → C → D → E → A
Tính từng góc:

Bài giải
Chiều rộng là 10 m, chiều dài là
3 x 10 = 30 (m)
Giảm chiều dài đi 5 m thì còn 25 m, thì bằng \(\frac{5}{2} \times 10\).
Vậy chiều dài 30 m, chiều rộng 10 m.
Diện tích hình chữ nhật là
30 . 10 = 300 (m²)
đáp số 300m²

góc xoy = 70 độ
góc xoz = 120 độ
số đo góc xoz :
xoz = 120 độ -70 độ = 50 độ
tia om là tia phân giác của góc xoy nên:
xom = xoy/2 = 70 độ /2 = 35 độ
tia on là tia phân giác của góc xoz nên:
xon = xoz/2 =120 độ/2 = 60 độ
góc mon là góc giữa tia om và on :
mon = 60 độ - 35 độ = 25 độ
két quả:
Trên cùng một nửa mặt phẳng bờ chứa tia Ox, ta có: \(\hat{xOy}<\hat{xOz}\left(70^0<100^0\right)\)
nên tia Oy nằm giữa hai tia Ox và Oz
=>\(\hat{xOy}+\hat{yOz}=\hat{xOz}\)
=>\(\hat{yOz}=100^0-70^0=30^0\)
Om là phân giác của góc xOy
=>\(\hat{xOm}=\hat{yOm}=\frac12\cdot\hat{xOy}=\frac12\cdot70^0=35^0\)
On là phân giác của góc xOz
=>\(\hat{xOn}=\hat{zOn}=\frac12\cdot\hat{xOz}=\frac12\cdot120^0=60^0\)
Trên cùng một nửa mặt phẳng bờ chứa tia Ox, ta có: \(\hat{xOm}<\hat{xOn}\left(35^0<60^0\right)\)
nên tia Om nằm giữa hai tia Ox và On
=>\(\hat{xOm}+\hat{mOn}=\hat{xOn}\)
=>\(\hat{mOn}=60^0-35^0=25^0\)

(tự vẽ hình )
câu 4:
a) có AB2 + AC2 = 225
BC2 = 225
Pytago đảo => \(\Delta ABC\)vuông tại A
b) Xét \(\Delta MAB\)và \(\Delta MDC\)
MA = MD (gt)
BM = BC ( do M là trung điểm của BC )
\(\widehat{AMB}=\widehat{CMD}\)( hai góc đối đỉnh )
=> \(\Delta MAB\)= \(\Delta MDC\) (cgc)
c) vì \(\Delta MAB\)= \(\Delta MDC\)
=> \(\hept{\begin{cases}AB=DC\\\widehat{MAB}=\widehat{MDC}\end{cases}}\)
=> AB// DC
lại có AB \(\perp\)AC => DC \(\perp\)AC => \(\Delta KCD\)vuông tại C
Xét \(\Delta\) vuông ABK và \(\Delta\)vuông KCD:
AB =CD (cmt)
AK = KC ( do k là trung điểm của AC )
=> \(\Delta\)vuông AKB = \(\Delta\)vuông CKD (cc)
=> KB = KD
d. do KB = KD => \(\Delta KBD\)cân tại K
=> \(\widehat{KBD}=\widehat{KDB}\)(1)
có \(\Delta ADC\)vuông tại C => \(AD=\sqrt{AC^2+DC^2}=15\)
=> MD = 7.5
mà MB = 7.5
=> MB = MD
=> \(\Delta MBD\)cân tại M
=> \(\widehat{MBD}=\widehat{MDB}\)(2)
Từ (1) và (2) => \(\widehat{KBD}-\widehat{MBD}=\widehat{KDB}-\widehat{MDB}\)hay \(\widehat{KBM}=\widehat{KDM}\)
Xét \(\Delta KBI\)và \(\Delta KDN\)có:
\(\widehat{KBI}=\widehat{KDN}\)(cmt)
\(\widehat{KBD}\)chung
KD =KB (cmt)
=> \(\Delta KBI\)= \(\Delta KDN\)(gcg)
=> KN =KI
=. đpcm
câu 5:
a) Xét \(\Delta ABM\)và \(\Delta MDC\):
MA=MD(gt)
MB=MC (M là trung điểm của BC)
\(\widehat{BMA}=\widehat{DMC}\)( đối đỉnh )
=> \(\Delta BMA=\Delta CMD\)(cgc)
b) Xét \(\Delta\)vuông ABC
có AM là đường trung tuyến của tam giác
=> \(AM=\frac{1}{2}BC\)mà \(BM=MC=\frac{1}{2}BC\)(do M là trung điểm của BC )
=> AM = BM = MC
có MA =MD => AM = MD =MB =MC
=> BM +MC = AM +MD hay BC =AD
Xét \(\Delta BAC\)và \(\Delta DCA\)
AB =DC
AC chung
BC =DC
=> \(\Delta BAC\)= \(\Delta DCA\)(ccc)
c. Xét \(\Delta ABM\)
BM=AM
\(\widehat{ABM}\)= 600
=> đpcm

câu a hơi kì nhỉ , theo mk thì phải là tam giác ABM = tam giác DCM chứ
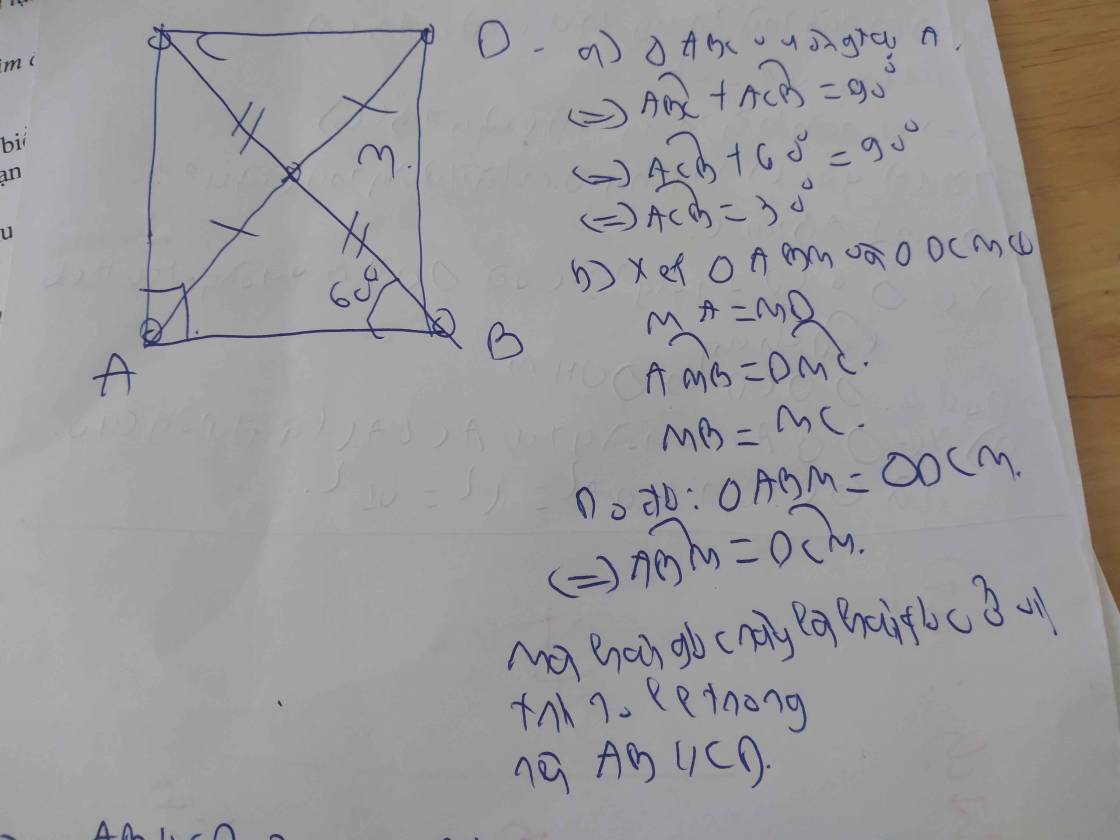
a) Xét \(\Delta ABM\) và \(\Delta DCM\)có :
AM=DM ( gt )
BM=MC ( gt )
\(\widehat{BMA}=\widehat{DMC}\) ( 2 góc đối đỉnh )
do đó \(\Delta ABM\) = \(\Delta DCM\) ( c.g.c )
b) Vì \(\Delta ABM=\Delta DCM\)( c/m trên )
\(\Rightarrow\widehat{ABM}=\widehat{DCM}\) ( 2 góc tương ứng )
mà 2 góc này ở vị trí so le trong
nên AB // BC

tu ve hinh :
a, xet tamgiac MBA va tamgiac MDC co :
goc BMA = goc DMC (doi dinh)
BM = CM do M la trung diem cua BC (GT)
MA = MD (GT)
=> tamgiac MBA = tamgiac MDC (c - g - c)
=> AB = DC (dn)
tamgiac MBA = tamgiac MDC => goc CDM = goc MAB ma 2 goc nay slt
=> AB // CD (dh)
b, co tamgiac ABC vuong tai A => AB | AC (dn) ; AB // DC (cau a)
=> AC | DC (dl) => tamgiac ACD vuong tai C (dn)
tamgiac MBA = tamgiac MDC => AB = CD (dn)
goc BAC = goc DCA = 90o do tamgiac ABC vuong tai A va tamgiac DCA vuong tai C
xet tamgiac ACB va tamgiac CAD co AC chung
=> tamgiac ACB = tamgiac CAD (2cgv)
=> BC = AD (dn)
M la trung diem cua BC => M la trung diem cua AD => AM = AD/2 (tc)
=> AM = BC/2