Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
ta có : BC = 2R ; AD = AE = r
nên 2R + r = BC + (AE + AD) = (BF + FC) + (AE + AD)
= (DB + EC) + (AE + AD) = (AD + DB) + (AE + EC)
= AB + AC ( đpcm)
a: xét (O) có
ΔCAB nội tiếp
AB là đường kính
Do đó: ΔCAB vuông tại C
b: Xét ΔCAB vuông tại C có \(cosBAC=\frac{AC}{AB}=\frac12\)
nên \(\hat{BAC}=60^0\)
ΔACB vuông tại C
=>\(CA^2+CB^2=AB^2\)
=>\(CB^2=AB^2-AC^2=\left(2R\right)^2-R^2=4R^2-R^2=3R^2\)
=>\(CB=R\sqrt3\)
c: Xét (O) có
MC,MB là các tiếp tuyến
Do đó: MC=MB
=>M nằm trên đường trung trực của CB(1)
ta có: OC=OB
=>O nằm trên đường trung trực của CB(2)
Từ (1),(2) suy ra MO là đường trung trực của CB
=>MO⊥CB
mà CA⊥CB
nên CA//OM
d: Gọi I là giao điểm của MA và CH, K là giao điểm của AC và MB
ΔACB vuông tại C
=>CA⊥CB tại C
=>CB⊥AK tại C
=>ΔKCB vuông tại C
Ta có: \(\hat{MCB}+\hat{MCK}=\hat{KCB}=90^0\)
\(\hat{MBC}+\hat{MKC}=90^0\) (ΔKCB vuông tại C)
mà \(\hat{MBC}=\hat{MCB}\) (ΔMBC cân tại M)
nên \(\hat{MCK}=\hat{MKC}\)
=>MC=MK
mà MC=MB
nên MB=MK(3)
ta có: KB⊥BA
CH⊥BA
DO đó: KB//CH
Xét ΔAMK có CI//MK
nên \(\frac{CI}{MK}=\frac{AI}{AM}\left(4\right)\)
Xét ΔAMB có IH//MB
nên \(\frac{IH}{MB}=\frac{AI}{AM}\) (5)
từ (3),(4),(5) suy ra CI=IH
=>I là trung điểm của CH
=>MA đi qua trung điểm I của CH
r r r A B C M N P I
Gọi M, N, P lần lượt là tiếp điểm của (I;r) với AB; BC; AC
Có: \(AB+AC-BC=AM+MB-BN-NC+CP+PA\)
Mà \(MB=BN\); \(NC=CP\); \(AM=PA\)
=> \(AB+AC-BC=2AM\)
Xét tứ giác MIPA có 3 góc vuông => MIPA là hình chữ nhật
=> \(AM=IP=r\)
=> \(r=AM=\frac{AB+AC-BC}{2}\)
Áp dụng bất đẳng thức cô si ta có :
b+c\(\ge2\)\(\sqrt{bc}\)\(\Rightarrow\)R(b+c)\(\ge2\)R.\(\sqrt{bc}\)\(\ge a\sqrt{bc}\)(quan hệ đường kính và dây cung 2R\(\ge\)BC=a)
Dấu "=" xảy ra khi:\(\left\{{}\begin{matrix}b=c\\BC=2R\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}CA=AB\\BC=2R\end{matrix}\right.\)
\(\Leftrightarrow\Delta ABC\) vuông cân tại A
Xét tam giác ABC có I là tâm đường tròn nội tiếp
\(S_{ABC}=S_{AIB}+S_{BIC}+S_{CIA}=\frac{1}{2}.AB.r+\frac{1}{2}.BC.r=\frac{1}{2}\)
\(AB+BC+CA.r=pr\)
P/s: Ko chắc
Tìm ba phân số khác nhau biết phân số thứ nhất và phân số thứ hai là 7/8,tổng của phân số thứ hai và phân số thứ ba là 8/7,tổng của phân số thứ nhất và phân số thứ ba là 8/9
BÀI LÀM
a, xét tứ giác ADOE có:
góc A= góc E=góc D=90O
mà ta thấy: OE=OD( bán kính = nhau)
vậy tứ giác ADOE là hình vuông (dhnb)
a) Dễ thấy tứ giác AEOD là hình chữ nhật (tứ giác có 3 góc vuông).
Mà OD = OE ( cùng bằng bán kính đường tròn nội tiếp tam giác ABC).
Nên tứ giác AEOD là hình vuông.
b) Gọi H là chân đường vuông góc kẻ từ O xuống BC.
Có SΔABC=SΔOAB+SΔOBC+SΔOAC
=12 OD.AB+12 OE.AC+12 OH.BC
=12 r.(AB+AC+BC)
=12 pr (pp là chu vi của tam giác ABCABC, rr là bán kính đường tròn nội tiếp).
c) Áp dụng định lý Pi-ta-go ta có: BC=√AB2+AC2=10(cm).
Diện tích tam giác ABC là: 12 AB.AC=12 .6.8=24(cm2).
Chu vi tam giác ABC là: 6+8+10=24(cm).
Suy ra: 24=12 .24.r⇔r=2(cm).
Chọn đáp án B
Vì tam giác ABC vuông tại A nên tâm đường tròn ngoại tiếp là trung điểm cạnh huyền BC, bán kính là R = BC/2
Theo định lý Pytago ta có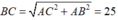
nên bán kính R = 25/2