Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

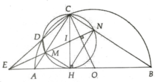
a, Tứ giác CMHN là hình chữ nhật
b, Ta có
O
C
A
^
=
O
A
C
^
C B A ^ = A C H ^ ; A C H ^ = C M N ^
=> O C A ^ + C M N ^ = 90 0
Vậy OC ⊥ MN
c, Ta có ∆IOC có E là trực tâm suy ra IN đi qua M và E (đpcm)
d, Ta có E M A ^ = C M N ^ ; C M N ^ = C B A ^ => ∆EMA:∆ENB
Tương tự ∆EMH:∆EHN => EM.EN = E H 2 ngoài ra , ∆EHC vuông tại H có HD là đường cao
=> E H 2 = ED.EC. Từ đó ta có đpcm

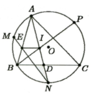
Gọi M,N,IM,N,I lần lượt là trung điểm AB,AC,ADAB,AC,AD
có M,N,IM,N,I thẳng hàng
AIEMAIEM nội tiếp⇒ˆAEF=ˆAMN⇒AEF^=AMN^(1)
AINFAINF nội tiếp ⇒ˆAFE=ˆANM⇒AFE^=ANM^(2)
(1,2)⇒ˆEDF=ˆEAF=90∘=ˆEOF⇒EDF^=EAF^=90∘=EOF^
⇒A,O,D,E,F⇒A,O,D,E,F cùng thuộc 1 đường tròn
b)
có △AEF△AEF luôn đồng dạng với △AMN△AMN cố định
⇒SAEF⇒SAEFmin khi AEAE min
có AE≥AMAE≥AM
⇒SAEF⇒SAEF min khi E≡M,F≡NE≡M,F≡N
lúc đó SAEF=bc8SAEF=bc8

a, HS tự chứng minh
b, M chính giữa A B ⏜
=> NE là phân giác B N A ^
=> B N A N = E B E A (tính chất đường phân giác) => BN.AE = NA.BE
c, HS tự chứng minh
d, Chứng minh ∆ABN:∆DBN => ĐPCM

Kẻ IG⊥AB tại G, kẻ IK⊥AC tại K
Xét ΔCKI vuông tại K và ΔCDI vuông tại D có
CI chung
\(\hat{KCI}=\hat{DCI}\)
Do đó: ΔCKI=ΔCDI
=>CK=CD và IK=ID
Xét ΔBGI vuông tại G và ΔBDI vuông tại D có
BI chung
\(\hat{GBI}=\hat{DBI}\)
Do đó: ΔBGI=ΔBDI
=>BG=BD
Xét ΔAKI vuông tại K và ΔAGI vuông tại G có
AI chung
\(\hat{KAI}=\hat{GAI}\)
Do đó: ΔAKI=ΔAGI
=>AK=AG
\(\frac{a+b-c}{2}=\frac{BC+AC-AB}{2}\)
\(=\frac{BD+CD+CK+KA-AG-GB}{2}=\frac{BD-BG+CD+CK+KA-AG}{2}\)
\(=\frac{CD+CK}{2}=\frac{2\cdot CD}{2}=CD\)