Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

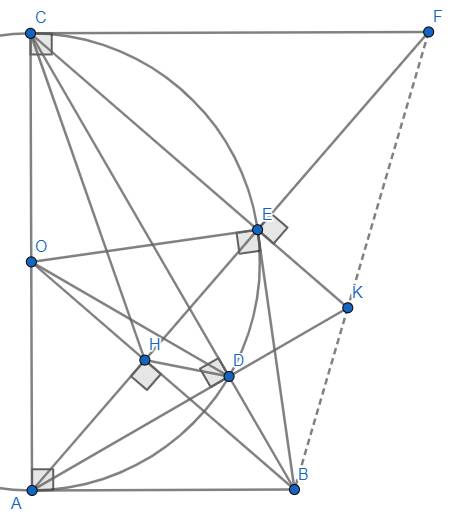
a) a1. Chứng minh \(BAOE\) là tứ giác nội tiếp.
Tứ giác \(BAOE:\left\{{}\begin{matrix}\hat{OEB}=90^o\left(\text{tiếp tuyến}\right)\\\hat{OAB}=90^o\left(gt\right)\end{matrix}\right.\)
\(\Rightarrow\hat{OEB}+\hat{OAB}=90^o+90^o=180^o\Rightarrow BAOE\) là tứ giác nội tiếp (đpcm).
a2. Chứng minh : \(BH.BO=BD.BC\).
Ta có : \(\hat{ADC}=90^o\) (góc nội tiếp chắn nửa đường tròn)
\(\Rightarrow AD\) là đường cao của \(\Delta ABC\) vuông tại \(A\Rightarrow BD.BC=AB^2\left(1\right).\)
Mặt khác : \(\left\{{}\begin{matrix}OA=OE=R\left(gt\right)\\AB=BE\left(\text{tính chất hai tiếp tuyến cắt nhau}\right)\end{matrix}\right.\)
\(\Rightarrow OB\) là đường trung trực của \(AE\Rightarrow\hat{AHB}=90^o\)
\(\Rightarrow AH\) là đường cao của \(\Delta ABC\) vuông tại \(A\Rightarrow BH.BO=AB^2\left(2\right).\)
Từ \(\left(1\right),\left(2\right)\Rightarrow BH.BO=BD.BC\) (đpcm).
b) b1. Chứng minh \(DHOC\) là tứ giác nội tiếp.
Tứ giác \(AHDB:\hat{AHB}=\hat{ADB}=90^o\left(cmt\right)\). Mà hai góc này có đỉnh kề nhau trong tứ giác và cùng nhìn cạnh \(AB\) nên đây là tứ giác nội tiếp \(\Rightarrow\hat{ABH}=\hat{ADH}.\)
Mà : \(\left\{{}\begin{matrix}\hat{ADH}+\hat{HDC}=90^o\left(=\hat{ADC}\left(cmt\right)\right)\\\hat{ABH}+\hat{HAB}=90^o\left(\text{hai góc phụ nhau}\right)\end{matrix}\right.\Rightarrow\hat{HDC}=\hat{HAB}\left(3\right).\)
Mặt khác : \(\hat{AOB}=\hat{HAB}\left(\text{cùng phụ }\hat{ABH}\right)\left(4\right).\)
Từ \(\left(3\right),\left(4\right)\Rightarrow\hat{AOB}=\hat{HDC}\Rightarrow DHOC\) là tứ giác nội tiếp (dấu hiệu nhận biết) (đpcm).
b2. Chứng minh : \(\hat{BHD}=\hat{OHC}\).
Do \(DHOC\) là tứ giác nội tiếp (cmt) \(\Rightarrow\hat{OCD}=\hat{BHD}\left(5\right)\) (cùng bù với \(\hat{OHD}\)) và \(\hat{OHC}=\hat{ODC}\left(6\right)\) (hai góc có đỉnh kề nhau cùng nhìn cạnh \(OC\)).
Mặt khác : \(OA=OD=R\Rightarrow\Delta OAD\) cân tại \(O\Rightarrow\hat{ODA}=\hat{OAD}.\)
Và : \(\left\{{}\begin{matrix}\hat{OAD}+\hat{OCD}=90^o\left(\text{hai góc phụ nhau}\right)\\\hat{ODA}+\hat{ODC}=90^o\left(=\hat{ADC}\right)\end{matrix}\right.\Rightarrow\hat{OCD}=\hat{ODC}\left(7\right).\)
Từ \(\left(5\right),\left(6\right),\left(7\right)\Rightarrow\hat{BHD}=\hat{OHC}\) (đpcm).
c) Chưa nghĩ ra ạ:)

a:
ΔABC vuông tại A có AB=AC
nên ΔABC vuông cân tại A
=>góc ABC=góc ACB=45 độ
góc BDA=1/2*sđ cung BA=90 độ
góc EAC=1/2*sđ cung CA=90 độ
BD vuông góc DA
CE vuông góc AE
mà D,A,E thẳng hàng
nên BD//CE
Xét tứ giác BDEC có
góc BDE+góc DEC+góc DBC+góc ECB=360 độ
=>góc DBC+góc ECB=180 độ
=>góc ECA+góc ACB+góc ABD+góc ABC=180 độ
=>góc ECA+góc ABD=90 độ
góc EAC+góc ECA=90 độ
mà góc DBA+góc ECA=90 độ
nên góc EAC=góc DBA
Xét ΔACE vuông tại E và ΔBAD vuông tại D có
AC=AB
góc EAC=góc DBA
=>ΔACE=ΔBAD
=>AD=CE
b: AD^2+AE^2
=CE^2+AE^2
=AC^2=16
bạn học thầy nguyên à?