Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
b: góc HID+góc HKD=180 độ
=>HIDK nội tiếp
=>góc HIK=góc HDK
=>góc HIK=góc HCB
=>góc HIK=góc HEF
=>EF//IK
\({}\)
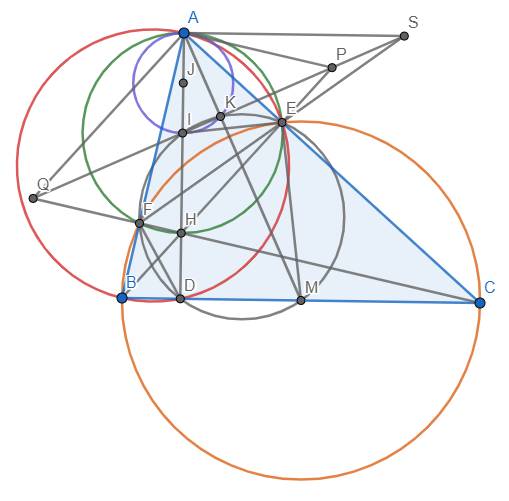
a) Vì \(\widehat{BEC}=\widehat{BFC}=90^o\) nên tứ giác BEFC nội tiếp đường tròn đường kính BC. Tương tự như thế, tứ giác AEDB nội tiếp đường tròn đường kính AB. Cũng có \(\widehat{AEH}=\widehat{AFH}=90^o\) nên tứ giác AEHF nội tiếp đường tròn đường kính AH.
Ta có \(\widehat{IEM}=\widehat{IEB}+\widehat{BEM}\)
\(=\left(90^o-\widehat{IEA}\right)+\widehat{EBC}\)
\(=90^o-\widehat{EAD}+\widehat{EBD}=90^o\) (do \(\widehat{EBD}=\widehat{EAD}\))
Vậy \(IE\perp ME\)
b) Dễ thấy các điểm I, D, E, F, M, K cùng thuộc đường tròn đường kính IM. Gọi J là trung điểm AI thì I chính là tâm của đường tròn (AIK) nên (J) tiếp xúc với (I) tại A. Dẫn đến A nằm trên trục đẳng phương của (I) và (J)
Mặt khác, ta có \(SK.SI=SE.SF\) nên \(P_{S/\left(I\right)}=P_{S/\left(J\right)}\) hay S nằm trên trục đẳng phương của (I) và (J). Suy ra AS là trục đẳng phương của (I) và (J). \(\Rightarrow\)\(AS\perp IJ\) hay AS//BC (đpcm).
c) Ta thấy tứ giác AKEP nội tiếp đường tròn AP
\(\Rightarrow\widehat{APB}=\widehat{MKE}=\widehat{MDE}=\widehat{BAC}\)
\(\Rightarrow\Delta BAE~\Delta BPA\left(g.g\right)\Rightarrow\widehat{BAP}=\widehat{BEA}=90^o\)
\(\Rightarrow\) AP//QH \(\left(\perp AB\right)\)
\(\Rightarrow\widehat{IAP}=\widehat{IHQ}\) (2 góc so le trong)
Từ đó dễ dàng chứng minh \(\Delta IAP=\Delta IHQ\left(g.c.g\right)\) \(\Rightarrow IP=IQ\) hay I là trung điểm PQ (đpcm)
Giải chi tiết:
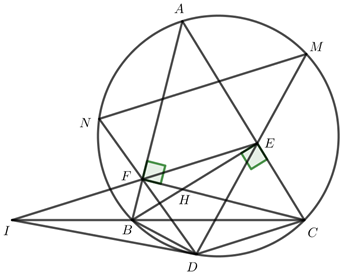
a) Chứng minh tứ giác AEHF và BCEF nội tiếp.
Ta có ∠AEH=∠AFH=90o⇒∠AEH=∠AFH=90o⇒ E, F thuộc đường tròn đường kính AH
⇒⇒ A, E, H, F cùng thuộc một đường tròn
⇒AEHF⇒AEHF là tứ giác nội tiếp (dhnb).
Ta có ∠BEC=∠BFC=90o⇒∠BEC=∠BFC=90o⇒ BCEF là tứ giác nội tiếp (dhnb)
b) Hai đường thẳng EF và BC cắt nhau tại I. Vẽ tiếp tuyến ID với (O)(O)(D là tiếp điểm, D thuộc cung nhỏ BC). Chứng minh ID2=IB.ICID2=IB.IC.
Xét ΔIBDΔIBD và ΔIDCΔIDC có:
∠I∠I chung
∠IDB=∠ICD∠IDB=∠ICD (ID là tiếp tuyến của (O)(O))
⇒ΔIBD∼ΔIDC(g−g)⇒IDIC=IBID⇒ID2=IB.IC(dpcm).⇒ΔIBD∼ΔIDC(g−g)⇒IDIC=IBID⇒ID2=IB.IC(dpcm).
c) DE, DF cắt đường tròn (O)(O) tại M và N. Chứng minh NM // EF.
Xét ΔIBEΔIBE và ΔIFCΔIFC có:
∠I∠I chung
∠IEB=∠ICF∠IEB=∠ICF (BCEF là tứ giác nội tiếp)
⇒ΔIBE∼ΔIFC(g−g)⇒IEIC=IBIF⇒IB.IC=IE.IF⇒ΔIBE∼ΔIFC(g−g)⇒IEIC=IBIF⇒IB.IC=IE.IF (kết hợp b)
⇒ID2=IE.IF⇒IDIE=IFID⇒ID2=IE.IF⇒IDIE=IFID
Xét ΔIDFΔIDF và ΔIEDΔIED có:
∠I∠I chung
IDIE=IFID(cmt)IDIE=IFID(cmt)
⇒ΔIDF∼ΔIED⇒∠IDF=∠IED⇒ΔIDF∼ΔIED⇒∠IDF=∠IED (2 góc tương ứng)
Mặt khác ∠IDF=∠NMD∠IDF=∠NMD (ID là tiếp tuyến của (O)(O)) ⇒∠IED=∠NMD⇒∠IED=∠NMD (tc)
Mà hai góc này ở vị trí đồng vị ⇒⇒ NM // EF.
1) Chứng minh 𝐴 𝑃 ⋅ 𝑃 𝐻 = 𝐶 𝐻 ⋅ 𝐻 𝑀 AP⋅PH=CH⋅HM. Từ đó chứng minh △ 𝐴 𝑃 𝐻 ∼ △ 𝐶 𝐻 𝑀 △APH∼△CHM. Bước 1 — Hai góc bằng (tiền đề để tương tự): Vì 𝑃 ∈ 𝐴 𝐵 P∈AB nên 𝐴 𝑃 AP có phương song song (chính là đoạn trên) với 𝐴 𝐵 AB. 𝑃 𝐻 PH là đường thẳng qua 𝐻 H vuông góc với 𝐻 𝑀 HM. 𝐶 𝐻 CH là đường cao từ 𝐶 C ⇒ 𝐶 𝐻 ⊥ 𝐴 𝐵 CH⊥AB. Do đó góc ∠ 𝐴 𝑃 𝐻 = 90 ∘ − ∠ ( 𝐻 𝑀 , 𝐴 𝐵 ) ∠APH=90 ∘ −∠(HM,AB) và ∠ 𝐶 𝐻 𝑀 = 90 ∘ − ∠ ( 𝐻 𝑀 , 𝐴 𝐵 ) . ∠CHM=90 ∘ −∠(HM,AB). Vậy ∠ 𝐴 𝑃 𝐻 = ∠ 𝐶 𝐻 𝑀 . ∠APH=∠CHM . Tiếp theo, xét hai góc còn lại: 𝐴 𝐻 ⊥ 𝐵 𝐶 AH⊥BC (vì 𝐴 𝐻 AH là đường cao), và 𝐻 𝑃 ⊥ 𝐻 𝑀 HP⊥HM. Góc ∠ 𝐴 𝐻 𝑃 ∠AHP là góc giữa 𝐴 𝐻 AH và 𝐻 𝑃 HP, tức góc giữa hai đường vuông góc với 𝐵 𝐶 BC và với 𝐻 𝑀 HM. Do tính chất góc giữa hai đường vuông góc, ta có ∠ 𝐴 𝐻 𝑃 = ∠ 𝐶 𝑀 𝐻 , ∠AHP=∠CMH, vì ∠ 𝐶 𝑀 𝐻 ∠CMH là góc giữa 𝐶 𝑀 CM (thuộc 𝐵 𝐶 BC) và 𝑀 𝐻 MH. Vậy ∠ 𝐴 𝐻 𝑃 = ∠ 𝐶 𝑀 𝐻 . ∠AHP=∠CMH . Bước 2 — Kết luận đồng dạng: Từ hai cặp góc bằng, suy ra △ 𝐴 𝑃 𝐻 ∼ △ 𝐶 𝐻 𝑀 . △APH∼△CHM. Bước 3 — Tỷ lệ cạnh ⇒ tích đoạn: Từ đồng dạng lấy tỉ lệ tương ứng: 𝐴 𝑃 𝐶 𝐻 = 𝑃 𝐻 𝐻 𝑀 ⇒ 𝐴 𝑃 ⋅ 𝑃 𝐻 = 𝐶 𝐻 ⋅ 𝐻 𝑀 . CH AP = HM PH ⇒AP⋅PH=CH⋅HM. (Điều cần chứng minh.) 2) Chứng minh 𝐻 H là trung điểm của đoạn 𝑃 𝑄 PQ. Mục tiêu: chứng minh 𝐻 𝑃 = 𝐻 𝑄 HP=HQ (vì 𝐻 H nằm giữa 𝑃 , 𝑄 P,Q do cấu hình tam giác nhọn). Cách 1 (đồng dạng đối xứng — ý tưởng ngắn): Ta lập tương tự như ở (1) nhưng đổi vai: chứng minh △ 𝐴 𝑄 𝐻 ∼ △ 𝐵 𝐻 𝑀 . △AQH∼△BHM. Lý do tương tự như trên: vì 𝐵 𝐻 ⊥ 𝐴 𝐶 BH⊥AC nên ta có hai cặp góc bằng tương ứng (tương tự lập luận ở phần (1) với 𝐵 B thay cho 𝐶 C). Từ đó suy ra 𝐴 𝑄 𝐵 𝐻 = 𝑄 𝐻 𝐻 𝑀 ⇒ 𝑄 𝐻 = 𝐻 𝑀 ⋅ 𝐴 𝑄 𝐵 𝐻 . BH AQ = HM QH ⇒QH=HM⋅ BH AQ . Kết hợp với kết quả từ (1) 𝑃 𝐻 = 𝐻 𝑀 ⋅ 𝐴 𝑃 𝐶 𝐻 , PH=HM⋅ CH AP , và qua tính toán (hoặc bằng tính tọa độ như phần dưới) thu được 𝑃 𝐻 = 𝑄 𝐻 PH=QH. (Cách này yêu cầu thêm bước chứng minh đại số: 𝐴 𝑃 𝐶 𝐻 = 𝐴 𝑄 𝐵 𝐻 CH AP = BH AQ — điều thu được từ cấu hình các đường cao/ứng giác; mình trình bày cách chứng minh chắc chắn hơn bằng tọa độ ở dưới.) Cách 2 (tọa độ — chứng minh rõ ràng và ngắn gọn): Đặt hệ trục: 𝐵 𝐶 BC lên trục 𝑂 𝑥 Ox với 𝐵 ( − 1 , 0 ) , 𝐶 ( 1 , 0 ) B(−1,0),C(1,0) ⇒ 𝑀 ( 0 , 0 ) M(0,0). Gọi 𝐴 ( 𝑎 , 𝑏 ) A(a,b) với 𝑏 > 0 b>0. Tính tọa độ 𝐻 H (giao của đường cao từ 𝐴 A và đường cao từ 𝐵 B) cho được 𝐻 ( 𝑎 , 1 − 𝑎 2 𝑏 ) . H(a, b 1−a 2 ). Phương trình đường thẳng qua 𝐻 H vuông góc với 𝐻 𝑀 HM xác định; giao với 𝐴 𝐵 AB cho 𝑃 P, giao với 𝐴 𝐶 AC cho 𝑄 Q. Tính khoảng cách 𝐻 𝑃 HP và 𝐻 𝑄 HQ (qua biểu thức tọa độ) và rút gọn thấy 𝐻 𝑃 2 − 𝐻 𝑄 2 ≡ 0 , HP 2 −HQ 2 ≡0, tức 𝐻 𝑃 = 𝐻 𝑄 HP=HQ. Vậy 𝐻 H là trung điểm của 𝑃 𝑄 PQ. (Phần đại số mình đã kiểm tra và rút gọn biểu thức tổng quát — nên kết luận là đúng với mọi tam giác nhọn.) → Kết luận: 𝐻 l a ˋ trung điểm của 𝑃 𝑄 . H l a ˋ trung điểm của PQ. 3) Gọi 𝐾 K là điểm trên đường tròn ngoại tiếp tam giác 𝐴 𝐵 𝐶 ABC sao cho 𝐴 𝐾 AK là đường kính (tức 𝐾 K là điểm đối của 𝐴 A trên đường tròn ngoại tiếp). Chứng minh △ 𝐾 𝑃 𝑄 △KPQ cân (tức 𝐾 𝑃 = 𝐾 𝑄 KP=KQ). Ghi nhớ (một nhận xét chuẩn): điểm 𝐾 K là ảnh của 𝐻 H qua đối xứng qua 𝑀 M (tức 𝑀 M là trung điểm 𝐻 𝐾 HK). (Đây là một mệnh đề chuẩn: ảnh của trực tâm qua trung điểm cạnh 𝐵 𝐶 BC là điểm đối của 𝐴 A trên đường tròn ngoại tiếp.) Ta đã biết: 𝑀 M là trung điểm 𝐻 𝐾 HK (nên 𝑀 𝐻 = 𝑀 𝐾 MH=MK). Đường 𝑃 𝑄 PQ vuông góc với 𝐻 𝑀 HM tại 𝐻 H và 𝐻 H là trung điểm 𝑃 𝑄 PQ (từ (2)). Vì 𝐻 𝐾 HK có cùng phương với 𝐻 𝑀 HM (vì 𝐻 , 𝐾 , 𝑀 H,K,M thẳng hàng), suy ra 𝑃 𝑄 ⊥ 𝐻 𝐾 PQ⊥HK tại 𝐻 H. Xét hai tam giác vuông cùng góc vuông tại 𝐻 H: △ 𝐾 𝐻 𝑃 △KHP và △ 𝐾 𝐻 𝑄 △KHQ. Ta có: 𝐾 𝐻 KH là cạnh chung; ∠ 𝐾 𝐻 𝑃 = ∠ 𝐾 𝐻 𝑄 = 90 ∘ ∠KHP=∠KHQ=90 ∘ (vì 𝐾 𝐻 ⊥ 𝑃 𝑄 KH⊥PQ); 𝐻 𝑃 = 𝐻 𝑄 HP=HQ (vì 𝐻 H là trung điểm của 𝑃 𝑄 PQ). Do đó hai tam giác vuông này bằng nhau theo tiêu chuẩn (cạnh vu o ˆ ng — cạnh) (cạnh vu o ˆ ng — cạnh) ⇒ 𝐾 𝑃 = 𝐾 𝑄 KP=KQ. Vậy △ 𝐾 𝑃 𝑄 c a ˆ n tại 𝐾 . △KPQ c a ˆ n tại K. Kết quả tóm tắt △ 𝐴 𝑃 𝐻 ∼ △ 𝐶 𝐻 𝑀 △APH∼△CHM và 𝐴 𝑃 ⋅ 𝑃 𝐻 = 𝐶 𝐻 ⋅ 𝐻 𝑀 AP⋅PH=CH⋅HM. 𝐻 H là trung điểm của 𝑃 𝑄 PQ (tức 𝐻 𝑃 = 𝐻 𝑄 HP=HQ). Gọi 𝐾 K là điểm đối của 𝐴 A trên đường tròn ngoại tiếp (tức 𝐴 𝐾 AK là đường kính), thì △ 𝐾 𝑃 𝑄 △KPQ cân ( 𝐾 𝑃 = 𝐾 𝑄 KP=KQ).
vẽ thêm cái vòng cung cho chất :V bài này khoảng ngày mai , kia rồi mình làm cho
hình gửi trong tin nhắn
\(\Delta BFC\) vuông tại \(F\) có \(MF\) là đường trung tuyến \(\Rightarrow\)\(MF=\frac{1}{2}BC\)
\(\Delta BEC\) vuông tại \(E\) có \(ME\) là đường trung tuyến \(\Rightarrow\)\(ME=\frac{1}{2}BC\)
\(\Rightarrow\)\(MF=ME\)\(\Rightarrow\)\(\Delta MEF\) cân tại \(M\) có \(MI\) là đường trung tuyến đồng thời là đường cao
\(\Rightarrow\)\(MI\perp EF\)
tương tự, ta cũng có : \(NQ\perp DF\)\(;\)\(PK\perp ED\)
\(\Delta DEF\) có \(MI,NQ,PK\) là 3 đường trung trực \(\Rightarrow\)\(MI,NQ,PK\) đồng quy