Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác AHBC có
E là trung điểm chung của AB và HC
=>AHBC là hình bình hành
Xét tứ giác ABCK có
D là trung điểm chung của AC và BK
=>ABCK là hình bình hành
b: Ta có: AHBC là hình bình hành
=>AH//BC và AH=BC
Ta có: ABCK là hình bình hành
=>AK//BC và AK=BC
Ta có: AH//BC
AK//BC
HA,AK có điểm chung là A
Do đó: H,A,K thẳng hàng
Ta có: AH=BC
AK=BC
Do đó: AH=AK
mà H,A,K thẳng hàng
nên A là trung điểm của HK

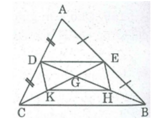
Tam giác ABC có hai đường trung tuyến BD và CE cắt nhau tại G nên G là trọng tâm tam giác ABC.
Ta có: GD = 1/2 GB (tính chất đường trung tuyến của tam giác)
GH = 1/2 GB (gt)
Suy ra: GD = GH
GE = 1/2 GC (tính chất đường trung tuyến của tam giác)
GK = 1/2 GC
Suy ra GE = GK
Tứ giác DEHK là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường).

Bài 1:
a: Xét tứ giác AHBC có
E la trung điểm chung của AB và CH
=>AHBC là hình bình hành
Xét tứ giác AKCB có
D là trung điểm chung của AC va KB
=>AKCB là hình bình hành
b: AHBC là hinh bình hanh
=>AH//BC và AH=BC
AKCB là hình bình hành
=>AK//BC và AK=BC
ta có: AH//BC
AK//BC
mà AH,AK có điểm chung là A
nên H,A,K thẳng hàng
Ta có: AK=BC
AH=BC
Do đó: AK=AH
mà H,A,K thẳng hàng
nên A là trung điểm của HK
Bài 2:
a: Ta có; AE+DE=AD
CF+FB=CB
ma AE=CF và AD=BC
nên DE=BF
Ta có: AM+MB=AB
CN+ND=CD
ma MB=ND va AB=CD
nên AM=CN
Xét ΔEAM và ΔFCN có
EA=FC
\(\hat{EAM}=\hat{FCN}\) (ABCD là hình bình hành)
AM=CN
Do đó: ΔEAM=ΔFCN
=>EM=FN
Xét ΔEDN và ΔFBM có
ED=FB
\(\hat{EDN}=\hat{FBM}\) (ABCD là hình bình hành)
DN=BM
Do đó: ΔEDN=ΔFBM
=>EN=FM
Xét tứ giác EMFN có
EM=FN
EN=FM
Do đó: EMFN là hình bình hành
b: Xét tứ giác AECF có
AE//CF
AE=CF
Do đó: AECF là hình bình hành
=>AC cắt EF tại trung điểm của mỗi đường(1)
ta có: EMFN là hình binh hành
=>EF cắt MN tại trung điểm của mỗi đường(2)
Ta có: ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường(3)
Từ (1),(2),(3) suy ra AC,EF,BD,MN đồng quy

a: Xét tứ giác AHBC có
E là trung điểm chung của AB và HC
=>AHBC là hình bình hành
Xét tứ giác AKCB có
D là trung điểm chung của AC và KB
=>AKCB là hình bình hành
b:AHBC là hình bình hành
=>AH//BC và AH=BC
AKCB là hình bình hành
=>AK//CB và AK=CB
AH//BC
AK//BC
mà AH,AK có điểm chung là A
nên H,A,K thẳng hàng
AH=BC
AK=BC
Do đó: AH=AK
H,A,K thẳng hàng
mà AH=AK
nên A là trung điểm của HK
Xét ΔABC có
BD,CE là trung tuyến
BD cắt CE tại G
=>G là trọng tâm
=>BG=2GD và CG=2GE
=>BG=GH và CG=GI
=>G là trung điểm chung của CI và BH
=>BIHC là hình bình hành