Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
góc CAD>90 độ
=>góc CED>90 độ
=>ED<CD
goc CDB=góc DAC+góc ACD
=>góc CDB>90 độ
=>CD<BC
=>ED<BC
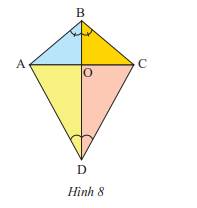
a) Tia BO là tia phân giác của \(\widehat {ABC}\) vì tia BO nằm giữa 2 tia BA và BC, tạo với 2 cạnh BA và BC 2 góc bằng nhau.
Tia DO là tia phân giác của \(\widehat {ADC}\) vì tia DO nằm giữa 2 tia DA và DC, tạo với 2 cạnh DA và DC 2 góc bằng nhau
b) Vì BO là tia phân giác của \(\widehat {ABC}\) nên \(\widehat {ABO} = \widehat {CBO} = \frac{1}{2}.\widehat {ABC} = \frac{1}{2}.100^\circ = 50^\circ \)
Vì DO là tia phân giác của \(\widehat {ADC}\)nên \(\widehat {ADO} = \widehat {CDO} = \frac{1}{2}.\widehat {ADC} = \frac{1}{2}.60^\circ = 30^\circ \)
Vậy \(\widehat {ABO} = 50^\circ ;\widehat {ADO} = 30^\circ \)
Bạn tham khảo ở đây nhé!!
https://h.vn/hoi-dap/question/269901.html
hok tốt!!
~
Vì góc bac là góc tú nên độ dài ab lớn
Mà d nằm giữa ba và e năm giữa ac nên
De<bc
- Xét tam giác ADE có:
Góc A tù (gt) nên góc ADE, góc AED là các góc nhọn.
=>Góc DEC là góc tù.
=>Góc EDC, góc DCE là các góc nhọn.
=>Góc DEC>Góc DCE.
=>DC>DE (quan hệ giữa góc và cạnh đối diện trong tam giác DEC). (1)
- Xét tam giác ADC có:
Góc A là góc tù (gt) nên góc ADC, góc ACD là các góc nhọn.
=> Góc BDC là góc tù.
=>Góc BCD, góc DBC là các góc nhọn.
=> Góc BDC>góc DBC.
=>BC>DC (quan hệ giữa góc và cạnh đối diện trong tam giác BDC) (2)
- Từ (1) và (2) suy ra: BC>DE
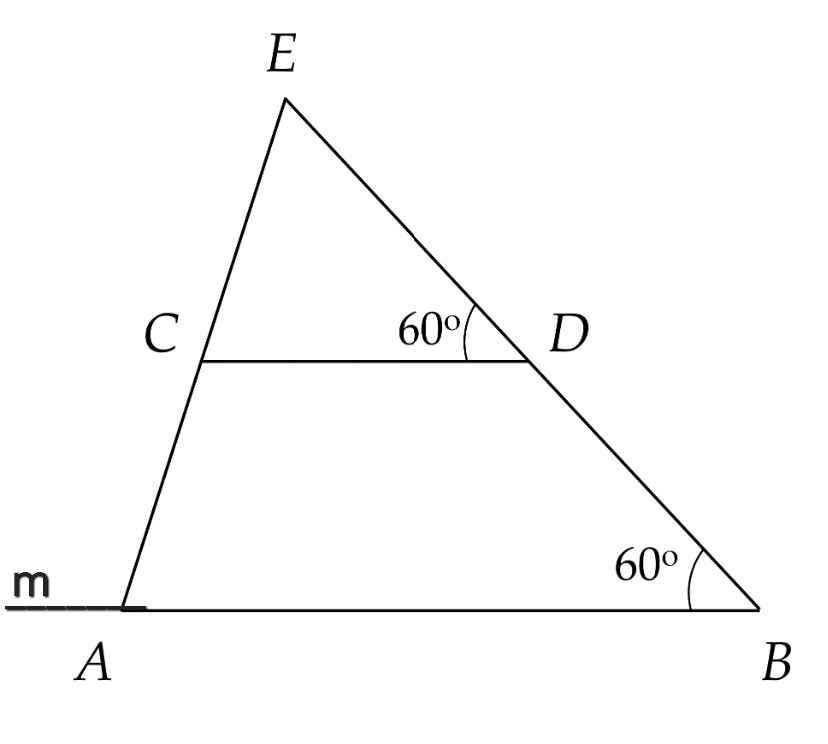
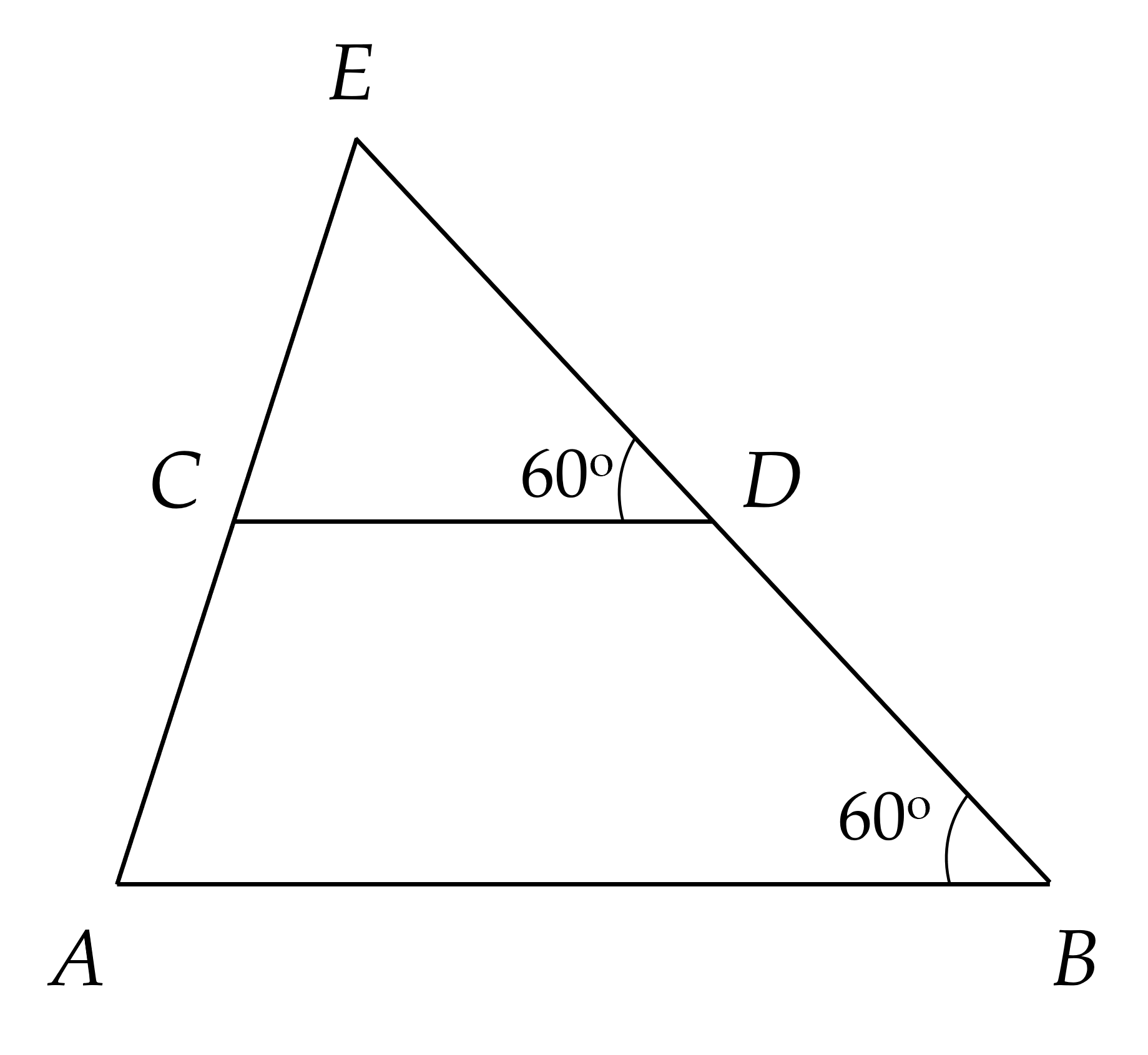
a) Ta có:
∠ABD = ∠CDE = 60⁰ (gt)
Mà ∠ABD và ∠CDE là hai góc so le trong
⇒ AB // CD
b) Vẽ tia Am là tia đối của tia AB
Do AB // CD
⇒ ∠mAC = ∠ACD (so le trong)
Mà ∠mAC + ∠BAC = 180⁰ (kề bù)
⇒ ∠ACD + ∠BAC = 180⁰
Giải thích các bước giải:
a)Xét tam giác BAD và tam giác BED:
BD:cạnh chung
^ABD=^EBD (vì BD là tia phân giác của ^ABC)
AB=BE(gt)
=>tam giác BAD=tam giác BED(c.g.c)
b)Từ tam giác BAD=tam giác BED(cmt)
=>AD=DE(cặp cạnh t.ứ)
và ^BAD=^BED(cặp góc .tứ),mà ^BAD=900 (^BAC=900)=>^BED=900
Xét tam giác DFA vuông ở A và tam giác DCE vuông ở E có:
AD=AE (cmt)
^ADF=^EDC (2 góc đối đỉnh)
=>tam giác DFA=tam giác DCE(cgv-gnk)
=>DF=DC(cặp cạnh t.ứ)
=>tam giác DFC cân tại D (dấu hiệu nhận biết tam giác cân)
c)Từ tam giác DFA=tam giác DCE (cmt)
=>AF=CE(cặp cạnh t.ứ)
Ta có: BE+CE=BC
BA+AF=BF
mà AF=CE(cmt),AB=AE(gt)
=>BC=BF
=>tam giác BFC cân tại B (dấu hiệu nhận biết tam giác cân)
=>^BCF=1800−FBC21800−FBC2 (tính chất tam giác cân) (1)
Vì AB=AE(gt)
=>tam giác ABE cân tại B (dấu hiệu nhận biết tam giác cân)
=>^BEA=1800−ABE21800−ABE2 (tính chất tam giác cân) (2)
Từ (1);(2);lại có ^ABE=^FBC
=>^BCF=^BEA,mà 2 góc này nằm ở vị trí đồng vị
=>AE//CF(dấu hiệu nhận biết 2 đg thẳng song song)
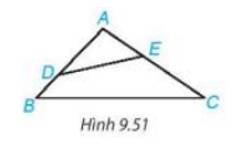
Ta có \(\widehat {BAC}\) là góc tù nên \(\widehat {ADE},\widehat {AED}\) là các góc nhọn
\( \Rightarrow \widehat {DEC}\) là góc tù
\( \Rightarrow DE < DC\) (quan hệ giữa góc và cạnh đối diện trong tam giác DEC). (1)
Xét tam giác ADC có:
\(\widehat {DAC}\) là góc tù nên \(\widehat {ADC},\widehat {ACD}\) là các góc nhọn
\( \Rightarrow \widehat {BDC}\) là góc tù.
\( \Rightarrow DC < BC\) (quan hệ giữa góc và cạnh đối diện trong tam giác BDC) (2)
Từ (1) và (2) suy ra: BC > DE