

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




BM = 3/2 BG, CN = 3/2 CG
Ta có BM + CN = 3/2 (BG + CG) > 3/2. BC = 3/2 x 12 = 18

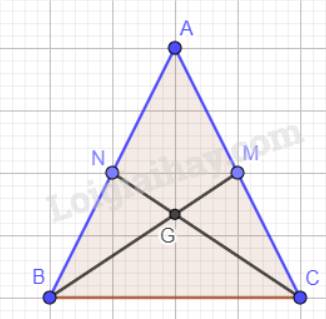
a) Tam giác ABC cân tại A nên AB = AC. M, N lần lượt là trung điểm của cạnh AC, AB nên AM = AN.
Xét tam giác ABM và tam giác ACN có: AM = AN; \(\widehat A\)chung; AB = AC.
Vậy \(\Delta ABM = \Delta ACN\)(c.g.c) hay BM = CN.
b) Xét tam giác ABC có G là giao điểm của hai đường trung tuyến BM và CN nên G là trọng tâm tam giác ABC. Do đó:
\(GB = \dfrac{2}{3}BM;GC = \dfrac{2}{3}CN\). Mà BM = CN nên GB = GC.
Vậy tam giác GBC cân tại G.

a: Xét ΔABC có
BM là đường trung tuyến
CN là đường trung tuyến
BM cắt CN tại G
DO đó:G là trọng tâm
=>BG=2/3BM; CG=2/3CN
\(BM+CN=\dfrac{2}{3}BG+\dfrac{2}{3}CG>\dfrac{2}{3}BC\)
b: BM=CN nên GB=GC
mà AB=AC
nên AG là đường trung trực của BC
=>AG\(\perp\)BC

a: Xét ΔABC có
N,M lần lượt là trung điểm của AB,AC
=>NM là đường trung bình của ΔABC
=>NM//BC và \(NM=\frac{BC}{2}\)
Xét ΔOBC có
P,Q lần lượt là trung điểm của OB,OC
=>PQ là đường trung bình của ΔOBC
=>PQ//BC và \(PQ=\frac{BC}{2}\)
Ta có: NM//BC
PQ//BC
Do đó: MN//PQ
Ta có: \(MN=\frac{BC}{2}\)
\(PQ=\frac{BC}{2}\)
Do đó: MN=PQ
b: Xét ΔMAB và ΔMCE có
\(\hat{MAB}=\hat{MCE}\) (hai góc so le trong, AB//CE)
MA=MC
\(\hat{AMB}=\hat{CME}\) (hai góc đối đỉnh)
Do đó: ΔMAB=ΔMCE
c: Gọi X là giao điểm của AF và BC
Xét ΔABC có
BM,CN là các đường trung tuyến
BM cắt CN tại O
Do đó: O là trọng tâm của ΔABC
=>AO cắt BC tại trung điểm của BC
=>X là trung điểm của BC
Xét ΔABC có
AX là đường trung tuyến
O là trọng tâm
Do đó: AO=2OX
mà AO=OF
nên OF=2OX
=>X là trung điểm của OF
Xét ΔABC có
BM là đường trung tuyến
O là trọng tâm
Do đó: BO=2OM
Xét tứ giác BOCF có
X là trung điểm chung của BC và OF
=>BOCF là hình bình hành
=>CF=BO=2OM

a: Xét ΔBNC và ΔCMB có
NB=MC
\(\widehat{NBC}=\widehat{MCB}\)
BC chung
Do đó; ΔBNC=ΔCMB
b: Sửa đề: Cm ΔANM cân tại A
Xét ΔANM có AN=AM
nên ΔANM cân tại A