
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a: O nằm trên đường trung trực của AB
=>OA=OB(1)
O nằm trên đường trung trực của AC
=>OA=OC(2)
từ (1),(2) suy ra OB=OC
Xét ΔABO và ΔACO có
AB=AC
BO=CO
AO chung
Do đó: ΔABO=ΔACO
=>\(\hat{ABO}=\hat{ACO}\)
Xét ΔOBD và ΔOCE có
OB=OC
\(\hat{OBD}=\hat{OCE}\overline{}\)
BD=CE
Do đó: ΔOBD=ΔOCE
b: ΔOBD=ΔOCE
=>OD=OE
=>O nằm trên đường trung trực của DE(3)
ta có: AD+DB=AB
AE+EC=AC
mà DB=EC và AB=AC
nên AD=AE
=>A nằm trên đường trung trực của DE(4)
Từ (3),(4) suy ra AO là đường trung trực của DE
c: Xét ΔABC có \(\frac{AD}{DB}=\frac{AE}{EC}\)
nên DE//BC
a)
\(O\) cách đều \(B\) và \(C\) ⇒ \(O B = O C\)
Giả thiết: \(B D = C E\)
Góc \(\angle D B O = \angle E C O\) do tam giác \(A B C\) cân, \(A O\) là trục đối xứng.
⇒ \(\triangle D O B = \triangle E O C\) (c.g.c).
b)
Từ (a) suy ra \(O D = O E\) ⇒ \(A O\) qua trung điểm \(D E\)
\(A O\) vuông góc \(D E\) (vì là trục đối xứng)
\(A O\) là đường trung trực của \(D E\).
c)
\(A O \bot B C\) và \(A O \bot D E\)
Hai đường cùng vuông góc với \(A O\) ⇒ DE\\BC
nhé bạn cảm ơn bí ẩn đã nhắc nhở\(\)

Câu a
Xét tam giác ABD và AMD có
AB = AM từ gt
Góc BAD = MAD vì AD phân giác BAM
AD chung
=> 2 tam guacs bằng nhau
Câu b
Ta có: Góc EMD bằng CMD vì góc ABD bằng AMD
Bd = bm vì 2 tam giác ở câu a bằng nhau
Góc BDE bằng MDC đối đỉnh
=> 2 tam giác bằng nhau

A B C D E 1 2
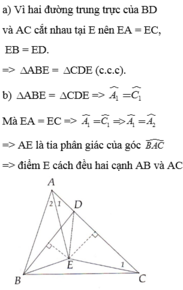
vì AC>AB mà AB=AD nên AD<AC mặt khác D thuộc AC nên D nằm giữa A và C
TA có: E thuộc đường trung trực của DB nên E cách đều D và B suy ra DE=DB
E thuộc đường trung trực của AC nên E cách đều A và C suy ra EA=EC
Xét \(\Delta AEB\)và \(\Delta CED\)
có\(\hept{\begin{cases}AB=DC\left(gt\right)\\BE=ED\left(cmt\right)\\AE=EC\left(cmt\right)\end{cases}}\)
\(\Rightarrow\Delta AEB=\Delta CED\left(c.c.c\right)\)
b, Do \(\Delta AEB=\Delta CED\left(c.c.c\right)\left(cmt\right)\)
Nên \(\Rightarrow\widehat{A_1}=\widehat{DCE}\)(2 góc tương ứng bằng nhau) (1)
Mà AE=EC suy ra tam giác AEC cân tại E
\(\Rightarrow\widehat{A_2}=\widehat{DCE}\)(2)
Từ 1 và 2 suy ra \(\widehat{A_1}=\widehat{A_2}\left(=\widehat{DCE}\right)\)
suy ra AE là phân giác của góc trong tại đỉnh A của tam giác ABC
2 đường kẻ hồng hồng là đường ttrung trực nha!
còn màu xanh lam là mk nối thêm cho ra tam giác