Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
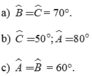
a) b) A B C B C A ABC cân tại A có C=B=50 ABC có A+B+C=180 A+50+50=180 A=80 ABC có A+B+C=180 70+2B=180 2B=180-70 2B=110 B=110:2 B=55 50 70
Answer:
a,
Ta có: \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)
Mà đề ra: \(\widehat{A}=40^o\)
\(\widehat{B}=\widehat{C}\) (Tam giác ABC cân tại A)
\(\Rightarrow40^o+\widehat{B}+\widehat{B}=180^o\)
\(\widehat{2B}=140^o\)
\(\widehat{B}=70^o\)
\(\Rightarrow\widehat{B}=\widehat{C}=70^o\)
C B A 40 độ
b,
Theo đề ra: Tam giác ABC cân tại A
\(\Rightarrow\widehat{B}=\widehat{C}=50^o\)
Ta có: \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)
\(\widehat{A}+100^o=180^o\)
\(\Rightarrow\widehat{A}=80^o\)
50 độ C B A
c,
Theo đề ra: Tam giác ABC cân tại A
\(\Rightarrow\widehat{C}=\widehat{B}=60^o\)
Ta có: \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)
\(\widehat{A}+120^o=180^o\)
\(\Rightarrow\widehat{A}=60^o\)
C A B 60 độ
Bài 1:
Xét \(\Delta ABC\) có:
\(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)(ĐL tổng 3 góc 1 \(\Delta\))
\(\Rightarrow30^o+70^o+\widehat{C}=180^o\) (Vì \(\widehat{A}=30^o;\widehat{B}=70^o\) (gt))
\(\Rightarrow\widehat{C}=180^o-30^o-70^o=80^o\)
Bài 2:
Xét \(\Delta ABC\) (vuông tại A) có:
\(\widehat{B}+\widehat{C}=90^o\) (Tc \(\Delta\) vuông)
\(\Rightarrow\widehat{B}+40^o=90^o\) (Vì \(\widehat{C}=40^o\) (gt))
\(\Rightarrow\widehat{B}=90^o-40^o=50^o\)
Giải:
+) Ta có: \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\) ( 3 góc của tam giác )
\(\Rightarrow30^o+70^o+\widehat{C}=180^o\)
\(\Rightarrow\widehat{C}=80^o\)
Vậy...
+) Ta có: \(\widehat{B}+\widehat{C}=90^o\) ( do tam giác có \(\widehat{A}=90^o\) )
\(\Rightarrow40^o+\widehat{B}=90^o\)
\(\Rightarrow\widehat{B}=50^o\)
Vậy...
vì goc B tuonng ung voi goc E =>GOC B=100*
vì goc A tuong ung voi goc D => D =20*
vì goc C tuong ung voi goc G =>goc G=60*
Đặ \(\hat{A}=a;\hat{B}=b;\hat{C}=c\)
Theo đề, ta có: 5a=3b=15c
=>\(\frac{5a}{15}=\frac{3b}{15}=\frac{15c}{15}\)
=>\(\frac{a}{3}=\frac{b}{5}=\frac{c}{1}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\frac{a}{3}=\frac{b}{5}=\frac{c}{1}=\frac{a+b+c}{3+5+1}=\frac{180}{9}=20\)
=>\(\begin{cases}a=20\cdot3=60\\ b=20\cdot5=100\\ c=20\cdot1=20\end{cases}\)
=>\(\hat{A}=60^0;\hat{B}=100^0;\hat{C}=20^0\)
AD là phân giác của góc BAC
=>\(\hat{BAD}=\hat{CAD}=\frac12\cdot\hat{BAC}=30^0\)
Xét ΔADC có \(\hat{ADB}\) là góc ngoài tại đỉnh D
nên \(\hat{ADB}=\hat{DAC}+\hat{DCA}=30^0+20^0=50^0\)
Tam giác \(A B C\) có các góc \(\hat{A} , \hat{B} , \hat{C}\) thỏa mãn:
\(5 \hat{A} = 3 \hat{B} = 15 \hat{C} .\)
1 . Tính số đo các góc của tam giác \(A B C\).
Gọi giá trị chung bằng \(k\). Ta có:
\(5 \hat{A} = 3 \hat{B} = 15 \hat{C} = k .\)
Suy ra:
\(\hat{A} = \frac{k}{5} , \hat{B} = \frac{k}{3} , \hat{C} = \frac{k}{15} .\)
Vì tổng ba góc của tam giác bằng \(180^{\circ}\):
\(\frac{k}{5} + \frac{k}{3} + \frac{k}{15} = 180.\)
Quy đồng mẫu số 15:
\(\frac{3 k}{15} + \frac{5 k}{15} + \frac{k}{15} = 180.\) \(\frac{9 k}{15} = 180.\) \(\frac{3 k}{5} = 180 \Rightarrow k = 180 \times \frac{5}{3} = 300.\)
Từ đó:
\(\hat{A} = \frac{300}{5} = 60^{\circ} ,\) \(\hat{B} = \frac{300}{3} = 100^{\circ} ,\) \(\hat{C} = \frac{300}{15} = 20^{\circ} .\)
Vậy \(\hat{A}=60^{\circ};\hat{B}=100^{\circ};\hat{C}=20^{\circ}.\)
\(\hat{B A D} = \hat{D A C} = 30^{\circ} .\)
\(\hat{B A D} = 30^{\circ} , \hat{B} = 100^{\circ} .\)
Suy ra góc còn lại:
\(\hat{A D B} = 180^{\circ} - \left(\right. 30^{\circ} + 100^{\circ} \left.\right) = 50^{\circ} .\)
Vậy \(\hat{A}=60^{\circ};\hat{B}=100^{\circ};\hat{C}=20^{\circ}.\)
CHO MÌNH XIN 1 TICK NHA\(\hat{A D B}=50^{\circ}\)
Bài 2:
Đặt số đo góc B là x, số đo góc C là y
Theo đề, ta có:
\(\left\{{}\begin{matrix}x+y=90\\x-y=24\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x=114\\x+y=90\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=57^0\\y=33^0\end{matrix}\right.\)
ΔABC=ΔDEF
=>\(\hat{A}=\hat{D}\)
mà \(\hat{A}=60^0\)
nên \(\hat{D}=60^0\)
ΔABC=ΔDEF
=>\(\hat{B}=\hat{E}\)
mà \(\hat{E}=80^0\)
nên \(\hat{B}=80^0\)
Xét ΔABC có \(\hat{A}+\hat{B}+\hat{C}=180^0\)
=>\(\hat{C}=180^0-60^0-80^0=100^0-60^0=40^0\)
ΔABC=ΔDEF
=>\(\hat{C}=\hat{F}\)
=>\(\hat{F}=40^0\)
a) bạn tính \(\widehat{B}=\widehat{C}=75^0\)
b)ta có: tam giác abc cân tại A
=> bc=ab=12cm
đúng nha
happy new year!@!!!!!!!!!
= 40°; b) 
= 50°; c) 
= 60°.