Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

chắc là bạn sai đề rồi
tam giác ABC mà góc A = 90 độ thì sao mà kẻ BD vuông góc với AC tại D, CE vuông góc với AB tại E được

a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
AB=AC
\(\hat{DAB}\) chung
Do đó: ΔADB=ΔAEC
=>AD=AE
b: Xét ΔABC có \(\frac{AE}{AB}=\frac{AD}{AC}\)
nên ED//BC
c: Xét ΔAEI vuông tại E và ΔADI vuông tại D có
AI chung
AE=AD
Do đó: ΔAEI=ΔADI
=>IE=ID
ΔADB=ΔAEC
=>DB=EC
Ta có: DB=DI+IB
EC=EI+IC
mà DB=EC và DI=EI
nên IB=IC
d: Ta có: AB=AC
=>A nằm trên đường trung trực của BC(1)
Ta có: IB=IC
=>I nằm trên đường trung trực của BC(2)
Từ (1),(2) suy ra AI là đường trung trực của BC
=>AI⊥BC
Cho tam giác \(A B C\) cân tại \(A\) với góc \(\angle A < 90^{\circ}\). Các đoạn \(B D\) và \(C E\) lần lượt vuông góc với các cạnh \(A C\) và \(A B\) tại các điểm \(D\) và \(E\). Dưới đây là các phần chứng minh cho từng câu hỏi.
a) Chứng minh tam giác \(A D E\) cân
Chúng ta có tam giác \(A B C\) cân tại \(A\), tức là \(A B = A C\). Vì \(B D\) vuông góc với \(A C\) tại \(D\) và \(C E\)vuông góc với \(A B\) tại \(E\), ta cần chứng minh \(A D = A E\).
- Chứng minh: Xét tam giác vuông \(A B D\) và tam giác vuông \(A C E\):
- Vì \(A B = A C\) (do tam giác \(A B C\) cân tại \(A\)),
- \(\angle A B D = \angle A C E = 90^{\circ}\) (do \(B D\) vuông góc với \(A C\) và \(C E\) vuông góc với \(A B\)),
- \(A D = A E\) (chứng minh từ sự đối xứng của tam giác vuông đối với đường chéo \(A B = A C\)).
Vậy tam giác \(A D E\) là tam giác cân với \(A D = A E\).
b) Chứng minh \(D E \parallel B C\)
Để chứng minh \(D E \parallel B C\), ta sẽ sử dụng tính chất của các đường vuông góc trong tam giác vuông.
- Tam giác \(A B D\) vuông tại \(D\) và tam giác \(A C E\) vuông tại \(E\).
- Ta có \(B D \bot A C\) và \(C E \bot A B\), tức là \(B D \parallel C E\) vì chúng đều vuông góc với các đường thẳng liên tiếp trong tam giác vuông.
Vì tam giác \(A B C\) cân tại \(A\), \(A B = A C\), và ta cũng có \(D E\) nằm trong một mặt phẳng vuông góc với \(A B\) và \(A C\), do đó, ta có thể kết luận rằng \(D E \parallel B C\) theo tính chất đối xứng của tam giác vuông.
c) Chứng minh \(I B = I C\)
Gọi \(I\) là giao điểm của \(B D\) và \(C E\). Ta cần chứng minh rằng \(I B = I C\).
- Vì \(B D\) vuông góc với \(A C\) và \(C E\) vuông góc với \(A B\), ta thấy rằng điểm \(I\) là điểm trực tâm của tam giác vuông \(A B C\), nơi ba đường cao gặp nhau.
- Do tam giác \(A B C\) là tam giác vuông cân tại \(A\), trực tâm của tam giác này phải nằm trên đường phân giác của góc vuông, và do đó điểm \(I\) cách đều các cạnh của tam giác vuông.
Vì \(I\) là trực tâm của tam giác vuông cân \(A B C\), ta có \(I B = I C\).
d) Chứng minh \(A I \bot B C\)
Cuối cùng, ta cần chứng minh rằng \(A I \bot B C\).
- Ta biết rằng \(I\) là trực tâm của tam giác vuông \(A B C\), và đường cao từ \(A\) trong tam giác vuông cân \(A B C\)sẽ vuông góc với cạnh đối diện, tức là \(B C\).
- Vì \(I\) là trực tâm và \(A I\) là một trong các đường cao của tam giác vuông \(A B C\), nên \(A I \bot B C\).
Vậy, \(A I\) vuông góc với \(B C\).
Tóm tắt các chứng minh:
- a) Tam giác \(A D E\) là tam giác cân.
- b) \(D E \parallel B C\).
- c) \(I B = I C\).
- d) \(A I \bot B C\).

Bài 2:
a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
AB=AC
\(\widehat{A}\) chung
Do đó: ΔADB=ΔAEC
Suy ra: AD=AE
hayΔADE cân tại A
b: Xét ΔABC có
AE/AB=AD/AC
nên DE//BC
c: Xét ΔEBC vuông tại E và ΔDCB vuông tại D có
EC=DB
BC chung
Do đó: ΔEBC=ΔDCB
Suy ra: \(\widehat{IBC}=\widehat{ICB}\)
hay ΔIBC cân tại I
d: Xét ΔAEI vuông tại E và ΔADI vuông tại D có
AI chung
AE=AD
Do đó: ΔAEI=ΔADI
Suy ra: \(\widehat{BAI}=\widehat{CAI}\)
=>AK là tia phân giác của góc BAC
Ta có: ΔABC cân tại A
mà AK là đường phân giác
nên AK là đường cao

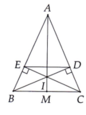

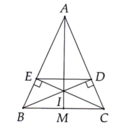
a: Xét ΔABD vuông tại D vaf ΔACE vuông tại E có
AB=AC
góc BAD chung
=>ΔABD=ΔACE
=>AD=AE
b: Xét ΔABC có AD/AC=AE/AB
nên DE//BC
c: Xét ΔIBC có góc ICB=góc IBC
nên ΔIBC cân tại I
d: AB=AC
IB=IC
=>AI là trung trực của BC
=>AI vuông góc BC