Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: O nằm trên đường trung trực của AB
=>OA=OB(1)
O nằm trên đường trung trực của AC
=>OA=OC(2)
từ (1),(2) suy ra OB=OC
Xét ΔABO và ΔACO có
AB=AC
BO=CO
AO chung
Do đó: ΔABO=ΔACO
=>\(\hat{ABO}=\hat{ACO}\)
Xét ΔOBD và ΔOCE có
OB=OC
\(\hat{OBD}=\hat{OCE}\overline{}\)
BD=CE
Do đó: ΔOBD=ΔOCE
b: ΔOBD=ΔOCE
=>OD=OE
=>O nằm trên đường trung trực của DE(3)
ta có: AD+DB=AB
AE+EC=AC
mà DB=EC và AB=AC
nên AD=AE
=>A nằm trên đường trung trực của DE(4)
Từ (3),(4) suy ra AO là đường trung trực của DE
c: Xét ΔABC có \(\frac{AD}{DB}=\frac{AE}{EC}\)
nên DE//BC
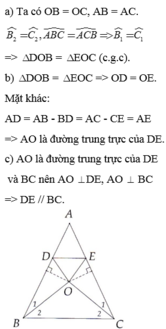
a)
\(O\) cách đều \(B\) và \(C\) ⇒ \(O B = O C\)
Giả thiết: \(B D = C E\)
Góc \(\angle D B O = \angle E C O\) do tam giác \(A B C\) cân, \(A O\) là trục đối xứng.
⇒ \(\triangle D O B = \triangle E O C\) (c.g.c).
b)
Từ (a) suy ra \(O D = O E\) ⇒ \(A O\) qua trung điểm \(D E\)
\(A O\) vuông góc \(D E\) (vì là trục đối xứng)
\(A O\) là đường trung trực của \(D E\).
c)
\(A O \bot B C\) và \(A O \bot D E\)
Hai đường cùng vuông góc với \(A O\) ⇒ DE\\BC
nhé bạn cảm ơn bí ẩn đã nhắc nhở\(\)

a: Xét ΔABD và ΔACE có
AB=AC
\(\widehat{A}\) chung
AD=AE
Do đó: ΔABD=ΔACE
Suy ra \(\widehat{ABD}=\widehat{ACE}\)
b:Xét ΔEBC và ΔDCB có
EB=DC
BC chung
EC=DB
Do đó: ΔEBC=ΔDCB
Suy ra: \(\widehat{ICB}=\widehat{IBC}\)
hay ΔIBC cân tại I
=>IB=IC
Ta có: EI+CI=EC
DI+BI=BD
mà BD=CE
và IB=IC
nên ID=IE

Em kham khảo link này nhé.
Câu hỏi của Đào Gia Khanh - Toán lớp 7 - Học toán với OnlineMath
a:
ΔABC cân tại A có AH là đường cao
nên AH là trung trực của BC
I nằm trên trung trực của AB
=>IA=IB
I nằm trên trung trực của BC
=>IB=IC
=>IA=IC
b: IA=IC
=>góc IAC=góc ICA
=>góc ICE=góc IAD
Xét ΔIEC và ΔIDA có
CE=DA
góc ICE=góc IAD
IC=IA
=>ΔIEC=ΔIDA
=>IE=ID