K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

YN
14 tháng 1 2020
A E B M D C 1 1 2 2 1 2
a, Ta có \(\Delta ABC\)cân tại A
=>AB=AC
+)Xét \(\Delta ABD\)và \(\Delta ACE\) có
AB=AC (cmt)
\(\widehat{BAC}\): chung
AD=AE (gt)
=> \(\Delta ABD\)= \(\Delta ACE\) (c-g-c)
=> \(\widehat{ABD}=\widehat{ACE}\) ( 2 góc t/ứ)
b, Ta có \(\hept{\begin{cases}\widehat{ABC}=\widehat{ACB}\\\widehat{ABD}=\widehat{ACE}\left(cmt\right)\end{cases}}\)(t/c t/g cân)
=> \(\widehat{B_2}=\widehat{C_2}\)
Xét \(\Delta IBC\)có \(\widehat{B_2}=\widehat{C_2}\)=> \(\Delta IBC\)cân tại I
Xin lỗi nhé mình chưa nghĩ ra câu b và câu c
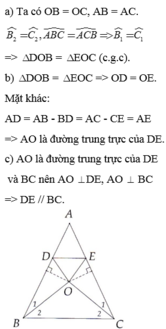

a: O nằm trên đường trung trực của AB
=>OA=OB(1)
O nằm trên đường trung trực của AC
=>OA=OC(2)
từ (1),(2) suy ra OB=OC
Xét ΔABO và ΔACO có
AB=AC
BO=CO
AO chung
Do đó: ΔABO=ΔACO
=>\(\hat{ABO}=\hat{ACO}\)
Xét ΔOBD và ΔOCE có
OB=OC
\(\hat{OBD}=\hat{OCE}\overline{}\)
BD=CE
Do đó: ΔOBD=ΔOCE
b: ΔOBD=ΔOCE
=>OD=OE
=>O nằm trên đường trung trực của DE(3)
ta có: AD+DB=AB
AE+EC=AC
mà DB=EC và AB=AC
nên AD=AE
=>A nằm trên đường trung trực của DE(4)
Từ (3),(4) suy ra AO là đường trung trực của DE
c: Xét ΔABC có \(\frac{AD}{DB}=\frac{AE}{EC}\)
nên DE//BC
a)
\(O\) cách đều \(B\) và \(C\) ⇒ \(O B = O C\)
Giả thiết: \(B D = C E\)
Góc \(\angle D B O = \angle E C O\) do tam giác \(A B C\) cân, \(A O\) là trục đối xứng.
⇒ \(\triangle D O B = \triangle E O C\) (c.g.c).
b)
Từ (a) suy ra \(O D = O E\) ⇒ \(A O\) qua trung điểm \(D E\)
\(A O\) vuông góc \(D E\) (vì là trục đối xứng)
\(A O\) là đường trung trực của \(D E\).
c)
\(A O \bot B C\) và \(A O \bot D E\)
Hai đường cùng vuông góc với \(A O\) ⇒ DE\\BC
nhé bạn cảm ơn bí ẩn đã nhắc nhở\(\)