Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
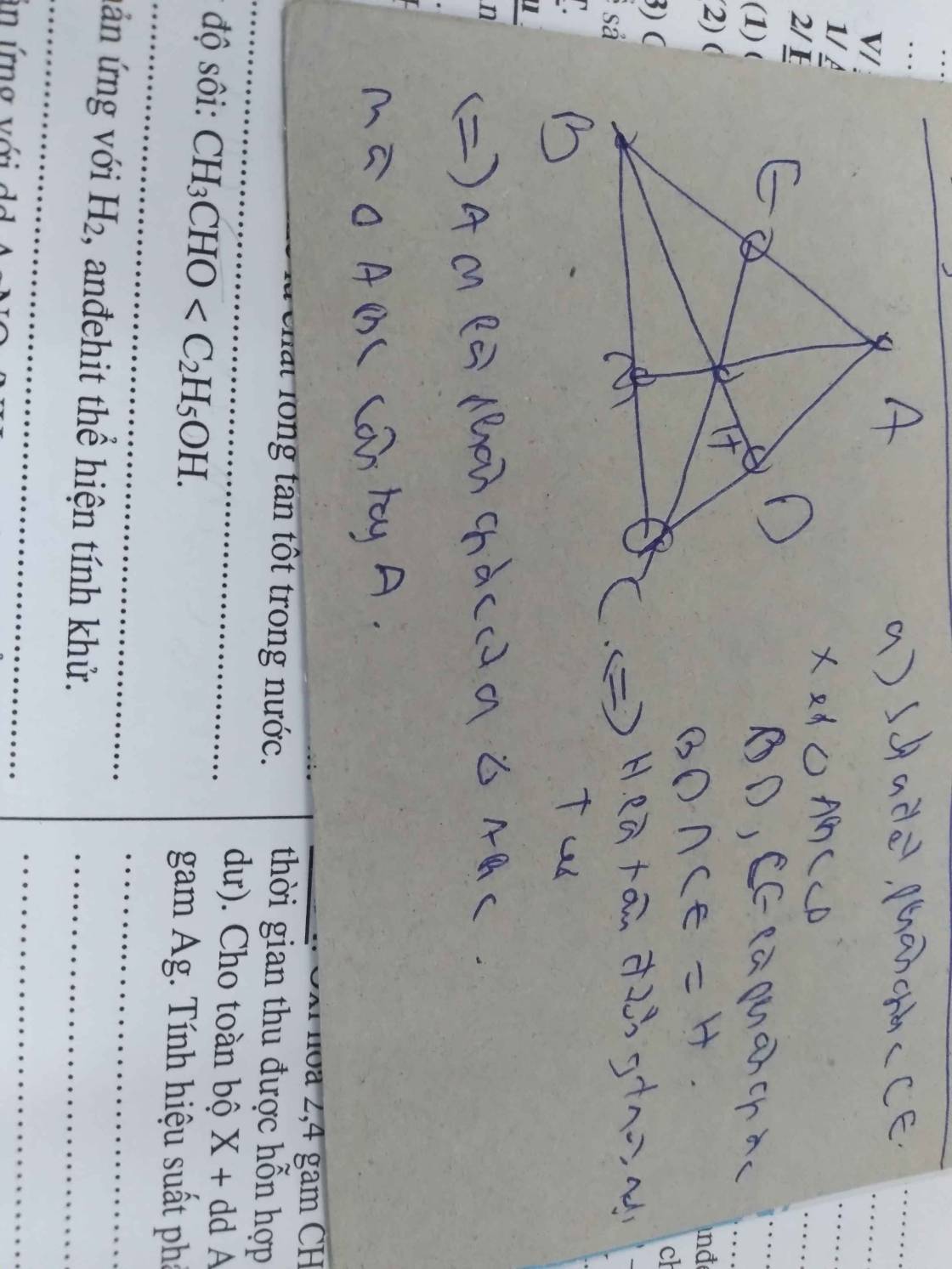
a)Xét tam giác ABD và tam giác BE
\(\widehat{ADE=}\widehat{AEC=}90^o\)
AB =AC tam giác chung
Vậy A chung ss...
=>Tam giác AD =A vuông tại E(cạnh huyền góc nhọn)
Vậy đường thẳng trên khác biệc mỗi 90*
b) Phân tích tam giác ABM
Ta có ABM gọi chung là H
Vậy thì trong đoạn trên H:
\(\widehat{HAB}=\widehat{HAC}\)(vuông tại A)
Vuông tại AC=AB (tam gs cân tại AB
Tam giác AHB =AHC (cân tại A)
=> Tam giác ABC =AHC (c.g.c)
Vậy : AMB = ACM
c)
Không ghi lại phần trình bày tất cả :
\(\Rightarrow\widehat{AED}=\frac{180^o-\widehat{A}}{2}\left(1\right)\)
tam giác ABC cân tại A
\(=>AMB=\frac{180-\widehat{A}}{4}\)(gấp đôi 1 phần)
_Đi qua đi lại xin 1 k thoi nha :>_
a) Xét 2 tam giác vuông: \(\Delta ABM\) và \(\Delta EBM\) có:
\(\widehat{ABM}=\widehat{EBM}\)(gt)
\(BM:\) CHUNG
suy ra: \(\Delta ABM=\Delta EBM\) (CH_GN)
b) \(\Delta ABM=\Delta EBM\)
\(\Rightarrow\)\(AB=EB\) => B thuộc trung trực AE
\(MA=ME\) => M thuộc trung tính AE
suy ra: BM là trung trực AE
c) \(\Delta EMC\) vuông tại E
=> \(EM< MC\)
mà \(EM=AM\)
\(\Rightarrow\)\(AM< MC\)
a: ΔABC cân tại A
=>\(\hat{ABC}=\hat{ACB}=\frac{180^0-\hat{BAC}}{2}=\frac{180^0-120^0}{2}=30^0\)
Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
=>\(\hat{HAB}=\hat{HAC}\)
=>AH là phân giác của góc BAC
=>\(\hat{BAH}=\hat{CAH}=\frac12\cdot\hat{BAC}=60^0\)
E nằm trên đường trung trực của AB
=>EA=EB
=>ΔEAB cân tại E
=>\(\hat{EAB}=\hat{EBA}=30^0\)
Ta có: \(\hat{BAE}<\hat{BAH}\left(30^0<60^0\right)\)
nên tia AE nằm giữa hai tia AB và AH
=>\(\hat{BAE}+\hat{HAE}=\hat{BAH}\)
=>\(\hat{HAE}=60^0-30^0=30^0\)
=>\(\hat{HAE}=\hat{DAE}\left(=30^0\right)\)
ED là đường trung trực của AB
mà D là trung điểm của AB
nên ED⊥AB tại D
Xét ΔAHE vuông tại H và ΔADE vuông tại D có
AE chung
\(\hat{HAE}=\hat{DAE}\)
Do đó: ΔAHE=ΔADE
=>HE=DE và AH=AD
Ta có: AH=AD
AD=DB
Do đó: AH=BD
Xét ΔBED vuông tại D và ΔAEH vuông tại H có
ED=EH
BD=AH
Do đó: ΔBED=ΔAEH
b: Xét ΔAHB vuông tại H và ΔADM vuông tại D có
AH=AD
\(\hat{HAB}\) chung
Do đó: ΔAHB=ΔADM
=>AB=AM
mà AB=AC
nên AM=AC
