Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: ΔOAC cân tại O
mà OM là đường cao
nên OM là phân giác của góc AOC
Xét ΔOAM và ΔOCM có
OA=OC
\(\hat{AOM}=\hat{COM}\)
OM chung
Do đó: ΔOAM=ΔOCM
=>\(\hat{OAM}=\hat{OCM}\)
=>\(\hat{OCM}=90^0\)
=>MC là tiếp tuyến của (O)
b: Gọi K là giao điểm của BC và AM
Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
=>AC⊥KB tại C
=>ΔACK vuông tại C
Ta có: \(\hat{MAC}+\hat{MKC}=90^0\) (ΔACK vuông tại C)
\(\hat{MCA}+\hat{MCK}=\hat{ACK}=90^0\)
mà \(\hat{MAC}=\hat{MCA}\)
nên \(\hat{MKC}=\hat{MCK}\)
=>MK=MC
mà MA=MC
nên MA=MK(1)
Ta có: CH⊥AB
KA⊥BA
Do đó: CH//KA
Xét ΔBAM có IH//AM
nên \(\frac{IH}{AM}=\frac{BI}{BM}\left(2\right)\)
Xét ΔBMK có CI//KM
nên \(\frac{CI}{KM}=\frac{BI}{BM}\left(3\right)\)
Từ (1),(2),(3) suy ra IH=IC
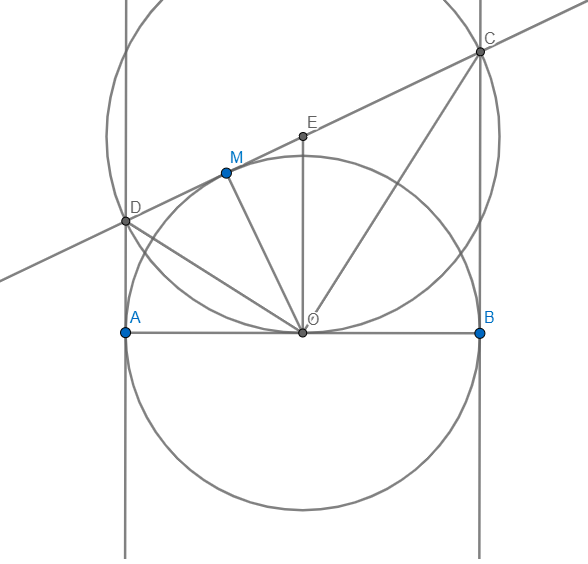
a) Chứng minh \(M C\) là tiếp tuyến của đường tròn
Vì \(A M\) là tiếp tuyến tại \(A\), nên \(A M \bot A O\).
Ta có:
- \(O M\) là đường thẳng đi qua \(O\) và vuông góc với \(A C\) (theo giả thiết).
- Tam giác \(A O C\) vuông tại \(A\) (do \(A B\) là đường kính nên \(\angle A C B = 90^{\circ}\)).
Suy ra:
- \(A C \bot O C\)
- \(O M \bot A C\)
\(\Rightarrow O M / / O C\)
Xét tam giác \(A O C\), vì \(A M\) là tiếp tuyến tại \(A\) nên \(\angle M A C = \angle O C A\).
Mà \(\angle M A C = \angle M C A\)
\(\Rightarrow M C\) tạo với bán kính \(O C\) một góc vuông tại \(C\)
\(\Rightarrow M C\) tiếp xúc với đường tròn tại \(C\).
→ MC là tiếp tuyến của đường tròn
b) Gọi \(H\) là hình chiếu của \(C\) trên \(A B\); \(I\) là giao điểm của \(M B\) và \(C H\). Chứng minh: \(C I = I H\).
Chứng minh:
- Tam giác \(A B C\) vuông tại \(A\) ⇒ \(H\) là chân đường vuông góc từ \(C\) xuống \(A B\) ⇒ \(H\) là hình chiếu của \(C\) lên đường kính → \(C H\) là đường cao ứng với cạnh huyền trong tam giác vuông \(A C B\).
- Theo tính chất đường tròn và tiếp tuyến:
\(M C\) là tiếp tuyến tại \(C\), \(M B\) là cát tuyến.
Ta có: \(M B^{2} = M C \cdot M A\) (định lý tiếp tuyến – cát tuyến). - Xét tam giác \(M C H\), đường thẳng \(M B\) cắt \(C H\) tại \(I\).
Sử dụng hệ thức của tam giác vuông nội tiếp đường tròn:
\(C H^{2} = C I \cdot I H\)
Nhưng vì tam giác \(A B C\) vuông tại \(A\) nên \(C H^{2} = A H \cdot H B\)
Mà theo tính chất đồng dạng của các tam giác \(\Rightarrow C I = I H\).
→ \(C I = I H\).

a)Gọi I là trung điểm của CD
Xét hình thang ACDB (AC//BD) có:\(\hept{\begin{cases}CI=ID\\AO=BO\end{cases}}\)
=>OI là đường tung bình của hình thang ACDB
=>\(OI=\frac{AC+BD}{2}=\frac{CD}{2}=CI=DI\)
=>Tam giác COD vuông tại O
=> đpcm
b)Kẻ OE vuông góc với CD,giao cuae CO và BD là F
Ta có tam giác ACO=Tam giác BFO( cạnh góc vuông-góc nhọn kề)
=>OC=OF
Xét tam giác CDF có:
CO=OF (cmt)
DO vuông góc với CF
=>tam giác CDF cân tại D
=>DO là phân giác góc CDF
=>góc EDO=BDO
=>tam giác EOD=tam giác BOD(Cạnh huyền - góc nhọn)
=>OE=OB
=>EO là bán kính (O) mà OE vuông góc với BC(cách vẽ)
=>CD là tiếp tuyến đường tròn đường kính AB

b) Vì DA,DM là tiếp tuyến \(\Rightarrow OD\) là phân giác \(\angle MOA\)
\(\Rightarrow\angle MOD=\dfrac{1}{2}\angle MOA\)
Vì CB,CM là tiếp tuyến \(\Rightarrow OC\) là phân giác \(\angle MOB\)
\(\Rightarrow\angle MOC=\dfrac{1}{2}\angle MOB\)
\(\Rightarrow\angle MOC+\angle MOD=\dfrac{1}{2}\left(\angle MOA+\angle MOB\right)\)
\(\Rightarrow\angle COD=\dfrac{1}{2}\angle AOB=\dfrac{1}{2}.180=90\)
c) Vì \(\angle COD=90\Rightarrow O\in\) đường tròn đường kính CD
Gọi E là tâm đường tròn đường kính CD \(\Rightarrow E\) là trung điểm CD
Ta có: E là trung điểm CD,O là trung điểm AB và ABCD là hình thang
\(\Rightarrow EO\parallel AD\) \(\Rightarrow EO\bot AB\Rightarrow AB\) là tiếp tuyến của đường tròn đường kính CD

ko biết vì chỉ đang học lớp 7 thui nha, ko biết để mà giúp
tui mới học lớp 8 .chưa học đường tròn.ko giúp được.sorry nha