Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

c: Gọi giao điểm của BC với Ax là K
BC\(\perp\)AC tại C
=>AC\(\perp\)BK tại K
=>ΔACK vuông tại C
\(\widehat{DKC}+\widehat{DAC}=90^0\)(ΔACK vuông tại C)
\(\widehat{DCK}+\widehat{DCA}=\widehat{KCA}=90^0\)
mà \(\widehat{DCA}=\widehat{DAC}\)(ΔDAC cân tại D)
nên \(\widehat{DKC}=\widehat{DCK}\)
=>DC=DK
mà DC=DA
nên DK=DA
=>D là trung điểm của AK
CH\(\perp\)AB
AK\(\perp\)AB
Do đó: CH//AK
Xét ΔOKD có CI//KD
nên \(\dfrac{CI}{KD}=\dfrac{OI}{OD}\left(1\right)\)
Xét ΔOAD có IH//AD
nên \(\dfrac{IH}{AD}=\dfrac{OI}{OD}\left(2\right)\)
Từ (1) và (2) suy ra \(\dfrac{CI}{KD}=\dfrac{IH}{AD}\)
mà KD=AD
nên CI=IH
=>I là trung điểm của CH

a:góc ABD=góc DCA
góc ABD=góc FAD(góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung AD)
góc FAD=góc CAD
=>góc ABD=góc CBD
=>BD là phân giác của góc ABE
mà góc ADB=90 độ
nên BD là đường cao
=>ΔBAE cân tại B
b: Xét ΔEAB có
AC,BD là các đường cao
AC cắt BD tại K
Do đó: K là trực tâm
=>EK vuông góc với BA
c: Xét ΔAKF có AD vừa là đường cao, vừa là phân giác
nên ΔAKF cân tại A
=>góc AKF=góc AFK=góc KFE
=>AK//FE
Xét tứ giác AKEF có
AK//FE
AF//KE
KE=KA
Do đó: AKEF là hình thoi

Tớ không vẽ hình được bạn tự vẽ nhé
a, Vì K thuộc đường tròn đường kính AB
=> AKB=90
Mà CHA=90
=> tứ giác AKNH nội tiếp
Vậy tứ giác AKNH nội tiếp
b,Vì 2 tiếp tuyến cắt nhau tại M
nên \(OM\perp AC\)
=>\(OM//CB\)
=> tam giác AMO đồng dạng tam giác HCB
=> ĐPCM
c, Tứ giác AMKI nội tiếp do AIM=AKM=90
KIC=AMK
MÀ AMK=KNC do AM song song CH
=> KIC=KNC
=> tứ giác KINC nội tiếp
=>KNI=KCI
Mà KCI=KBA
=> KNI=KBA
=> IN song song AB
Vậy IN song song AB
Mình không viết kí hiệu góc nên bạn thông cảm

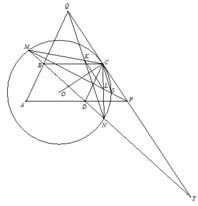
1). Gọi MN giao PQ tại T. Theo định lí Thales, ta có T P T C = T D T B = T C T Q .
Từ đó T C 2 = T P . T Q .
Do TC là tiếp tuyến của (O), nên T C 2 = T M . T N .
Từ đó T M . T N = T C 2 = T P . T Q , suy ra tứ giác MNPQ nội tiếp.
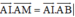 và
và 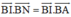
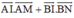 theo R.
theo R.
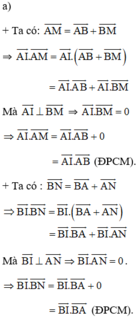

a: Gọi H là trung điểm của CD
=>H là tâm đường tròn đường kính CD
Xét (O) có
CM,CA là các tiếp tuyến
Do đó: CM=CA và OC là phân giác của góc MOA
Xét (O) có
DM,DB là các tiếp tuyến
Do đó: DM=DB và OD là phân giác của góc MOB
ta có: OC là phân giác của góc MOA
=>\(\hat{MOA}=2\cdot\hat{MOC}\)
ta có: OD là phân giác của góc MOB
=>\(\hat{MOB}=2\cdot\hat{MOD}\)
ta có: \(\hat{MOA}+\hat{MOB}=180^0\) (hai góc kề bù)
=>\(2\left(\hat{MOC}+\hat{MOD}\right)=180^0\)
=>\(2\cdot\hat{COD}=180^0\)
=>\(\hat{COD}=90^0\)
=>O nằm trên đường tròn đường kính CD
hay O nằm trên (H)
Xét hình thang ABDC có
O,H lần lượt là trung điểm của AB,CD
=>OH là đường trung bình của hình thang ABDC
=>OH//AC//BD và \(OH=\frac{AC+BD}{2}\)
ta có: OH//AC
CA⊥AB
Do đó: OH⊥AB
=>(H) tiếp xúc với AB tại O
b: \(C_{ABDC}=AC+CD+DB+AB\)
=CM+CD+DM+AB
=CD+CD+AB
=2CD+AB
Kẻ CK⊥BD tại K
=>CK<=CD
CK⊥BD
AB⊥BD
Do đó: CK//AB
Xét tứ giác ABKC có
KC//AB
AC//BK
Do đó: ABKC là hình bình hành
=>KC=AB=2R
Để chu vi hình thang ABDC nhỏ nhất thì 2CD+AB nhỏ nhất
mà AB cố định
nên 2CD nhỏ nhất
=>CD nhỏ nhất
mà CD<=CK=2R
nên CD nhỏ nhất khi CD=2R
mà OM=R
nên OM=1/2CD
ΔCOD vuông tại O
mà OH là đường trung tuyến
nên \(OH=\frac12CD\)
=>OM=OH
=>M trùng với H
=>MO⊥AB tại O
=>M là điểm chính giữa của cung AB
c: \(C_{ABDC}=2CD+AB\)
=>2CD+4=14
=>2CD=10
=>CD=5(cm)