Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

cạnh góc vuông lớn 7.5
cạnh huyền \(\frac{3}{2}\sqrt{41}\)
hình chiếu có 1 thôi vì chung đỉnh 900/41 :) số hơi lẻ

Gọi độ dài cạnh góc vuông thứ nhất là x(cm)
(Điều kiện: x>0)
Độ dài cạnh huyền là \(x:\frac{20}{29}=\frac{29}{20}x\left(\operatorname{cm}\right)\)
Độ dài cạnh góc vuông thứ hai là:
\(\sqrt{\left(\frac{29}{20}x\right)^2-x^2}=\sqrt{\left(\frac{29}{20}x-x\right)\left(\frac{29}{20}x+x\right)}=\sqrt{\frac{9}{20}x\cdot\frac{49}{20}x}=\frac{21}{20}x\) (cm)
Chu vi tam giác vuông là 210cm nên ta có:
\(x+\frac{29}{20}x+\frac{21}{20}x=210\)
=>3,5x=210
=>x=210:3,5=60(nhận)
vậy: Độ dài cạnh góc vuông thứ nhất là 60cm
Độ dài cạnh góc vuông thứ hai là \(60\cdot\frac{21}{20}=63\left(\operatorname{cm}\right)\)
Độ dài cạnh huyền là \(\frac{29}{20}\cdot60=3\cdot29=87\left(\operatorname{cm}\right)\)

Gọi độ dài cạnh góc vuông thứ 2 là x>0 (cm)
\(\Rightarrow\) Độ dài cạnh huyền là \(x+2\) (cm)
Theo định lý Pitago ta có:
\(4^2+x^2=\left(x+2\right)^2\)
\(\Leftrightarrow16+x^2=x^2+4x+4\)
\(\Leftrightarrow4x=12\Rightarrow x=3\)
Vậy độ dài cạnh huyền là \(3+2=5\left(cm\right)\)

Theo đề, ta có:
\(5^2+\left(a-1\right)^2=a^2\)
\(\Leftrightarrow a^2=a^2-2a+1+25\)
=>a=13
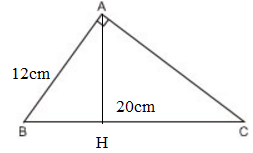
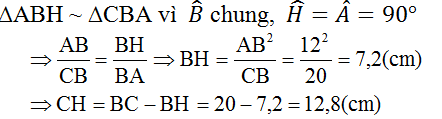
ΔABC vuông tại A có đường cao AH, BC = 20cm, AB = 12cm. Ta tính HC.
ΔABC và ΔHBA có: