Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

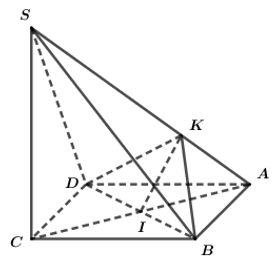
a có \(\angle \left(\right. S C , \left(\right. A B C D \left.\right) \left.\right) = 45^{\circ}\).
Nghĩa là hình chiếu của \(S\) xuống đáy nằm trên đường chéo \(B D\).
Xét tam giác cân \(S A B\), do tính đối xứng ⇒ khoảng cách từ \(A\) đến \(\left(\right. S C D \left.\right)\) chính bằng nửa cạnh hình vuông:
\(d\left(\right.A,\left(\right.SCD\left.\right)\left.\right)=\frac{a}{2}\)
Với \(M\) là trung điểm \(S A\), khoảng cách giảm đi một nửa:
\(d\left(\right.M,\left(\right.SCD\left.\right)\left.\right)=\frac{a}{4}\)
Đáp số
\(d \left(\right. A , \left(\right. S C D \left.\right) \left.\right) = \frac{a}{2}\)
\(d \left(\right. M , \left(\right. S C D \left.\right) \left.\right) = \frac{a}{4}\)

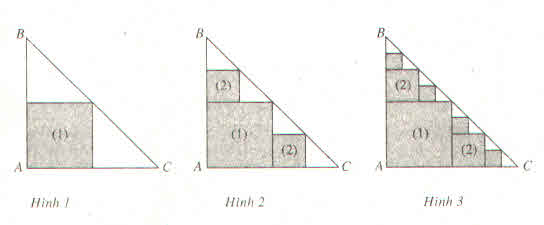
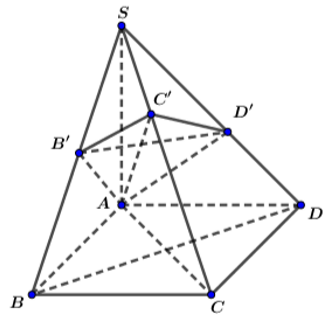
a) Hình vuông thứ nhất có cạnh bằng nên u1 = (
)2 =
.
Hình vuông thứ hai có cạnh bằng nên u2 = (
)2 =
.
Hình vuông thứ ba có cạnh bằng nên u3 = (
)2 =
.
Tương tự, ta có un =
b) Dãy số (un) là một cặp số nhân lùi vô hạn với u1 = và q =
. Do đó
lim Sn = .

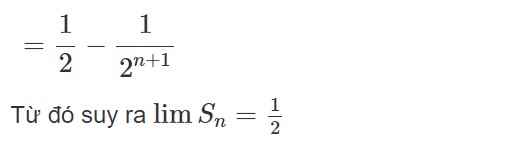

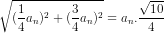 với n ε N*.
với n ε N*. 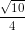










Chọn B
Số cách chọn ra 3 đỉnh trong số 25 đỉnh của các hình vuông đơn vị là: C 25 3
TH1: 3 đỉnh nằm trên cùng 1 hàng hoặc cùng 1 cột là: 5 C 5 3 + 5 C 5 3
TH2: 3 đỉnh nằm trên một trong các đường chéo của hình vuông kích thước 4x4, 3x3, 2x2 sao cho các đường chéo ấy không trùng nhau là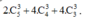
TH3: 3 đỉnh nằm trên một trong các đường chéo của hình chữ nhật kích thước 2x4. Số hình chữ nhật đó là 6. Do đó số cách chọn là 12
Vậy số tam giác được tạo thành là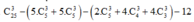 = 2148
= 2148