Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Ta có: DC//AB
=>\(\hat{CDA}+\hat{DAB}=180^0\)
=>\(2\cdot\hat{DAB}+\hat{DAB}=180^0\)
=>\(3\cdot\hat{DAB}=180^0\)
=>\(\hat{DAB}=60^0\)
=>\(\hat{ADC}=2\cdot60^0=120^0\)
Ta có: ABCD là hình thang cân
=>\(\hat{CBA}=\hat{DAB}=60^0\) ; \(\hat{ADC}=\hat{DCB}=120^0\)
ΔCBA vuông tại C
=>\(\hat{CAB}+\hat{CBA}=90^0\)
=>\(\hat{CAB}=90^0-60^0=30^0\)
Ta có: tia AC nằm giữa hai tia AB và AD
=>\(\hat{DAC}+\hat{BAC}=\hat{DAB}\)
=>\(\hat{DAC}=60^0-30^0=30^0\)
Ta có: tia AC nằm giữa hai tia AD và AB
mà \(\hat{DAC}=\hat{BAC}\left(=30^0\right)\)
nên AC là phân giác của góc DAB
b: Ta có: \(\hat{DCA}=\hat{CAB}\) (hai góc so le trong, AB//CD)
\(\hat{DAC}=\hat{CAB}\)
Do đó: \(\hat{DCA}=\hat{DAC}\)
=>DA=DC=a
Ta có: ABCD là hình thang cân
=>DA=CB
=>CB=a
Kẻ DH⊥AB tại H và CK⊥AB tại K
Xét ΔDHA vuông tại H và ΔCKB vuông tại K có
DA=CB
\(\hat{DAH}=\hat{CBK}\)
Do đó: ΔDHA=ΔCKB
=>DH=CK và AH=BK
DH⊥AB
CK⊥AB
Do đó: DH//CK
Xét tứ giác DCKH có
DC//HK
DH//CK
Do đó: DCKH là hình bình hành
=>DC=HK=a
Gọi M là trung điểm của BC
Trên tia đối của tia MK, lấy I sao cho MK=MI
Xét tứ giác BKCI có
M là trung điểm chung của BC và KI
=>BKCI là hình bình hành
Hình bình hành BKCI có \(\hat{BKC}=90^0\)
nên BKCI là hình chữ nhật
=>BC=KI
mà \(KM=MI=\frac{KI}{2};MB=MC=\frac{BC}{2}\)
nên KM=MI=MB=MC=BC/2=KI/2
Xét ΔBMK có MK=MB và \(\hat{MBK}=60^0\)
nên ΔMBK đều
=>BK=MB=BC/2
=>BK=a/2
TA có: AB=AH+HK+KB
=a/2+a+a/2
=2a
Chu vi hình thang ABCD là:
AB+BC+CD+DA
=2a+a+a+a
=5a
ΔCKB vuông tại K
=>\(CK^2+KB^2=CB^2\)
=>\(CK^2=a^2-\left(\frac{a}{2}\right)^2=\frac{3a^2}{4}\)
=>\(CK=\frac{a\sqrt3}{2}\)
Diện tích hình thang BCDA là:
\(S_{DCBA}=\frac12\cdot CK\cdot\left(DC+BA\right)=\frac12\cdot\frac{a\sqrt3}{2}\cdot\left(a+2a\right)=\frac{a\sqrt3}{4}\cdot3a=3\sqrt3\cdot\frac{a^2}{4}\)

a) DDBC vuông có B C D ^ = 2 B D C ^ nên A D C ^ = B C D ^ = 60 0 và D A B ^ = C B A ^ = 120 0
b) Tính được DC = 2.BC = 12cm, suy ra PABCD = 30cm.
Hạ đường cao BK, ta có BK = 3 3 c m .
Vậy SABCD = 27 3 c m 2
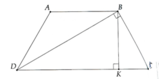

Xét tam giác BCD
^CBD=180-^BCD-^BDC=180-60-30=90 => tam giác BCD vuông tại B
=> BC=CD/2 (Trong tam giác vuông cạnh đối diện góc 30 độ =1/2 cạnh huyền) => CD=2.BC (1)
+ AB//CD => ^ABC+^BCD=^ABC+60=180 (Hai đường thẳng // bị cắt bởi 1 cát tuyến thì hai góc trong bù nhau)
=> ^ABC=180-60=120 => ^ABD=^ABC-^CBD=120-90=30
+ Xét tam giác ABD có ^ADB=^ABD=30 => t/g ABD cân tại A => AD=AB (2)
+ Do hình thang ABCD cân => AD=BC (3)
+ Chu vi hình thang = AB+BC+CD+AD (4)
Từ (1) (2) (3) (4) => CV hình thang ABCD=5.BC=20 cm
=> BC=20:5=4 cm
=> AB=BC=AD=4 cm
CD=2.BC=2.4=8 cm

A B C D
+ Xét tam giác BCD
^CBD=180-^BCD-^BDC=180-60-30=90
=> tam giác BCD vuông tại B
=> BC=CD/2 (Trong tam giác vuông cạnh đối diện góc 30 độ =1/2 cạnh huyền)
=> CD=2.BC (1) + AB//CD
=> ^ABC+^BCD=^ABC+60=180 (Hai đường thẳng // bị cắt bởi 1 cát tuyến thì hai góc trong bù nhau)
=> ^ABC=180-60=120
=> ^ABD=^ABC-^CBD=120-90=30
+ Xét tam giác ABD có
^ADB=^ABD=30
=> t/g ABD cân tại A => AD=AB (2)
+ Do hình thang ABCD cân
=> AD=BC (3)
+ Chu vi hình thang = AB+BC+CD+AD (4)
Từ (1) (2) (3) (4) => CV hình thang ABCD=5.BC=20 cm
=> BC=20:5=4 cm
=> AB=BC=AD=4 cm
CD=2.BC=2.4=8 cm
^ như này là góc nhé
Hình thang cân có 2góc ở đáy bằng nhau => C^=D^=45° và A^=B^=135°
Kẻ AH vuông CD, BK vuông CD.
Theo tính chất đoạn chắn ta có AB//HK và AB=HK=13cm
=>DH=BK=(DC-AB)/2=6cm
Tam giác ADH vuông tại H có góc D=45° nên là tam giác vuông cân => AH=DH=6cm
Ta có diện tích hình thang=(AB+CD)*AH/2=(13+25)*6/2=114cm^2
làm sai rồi. tính cũng sai