Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn D.
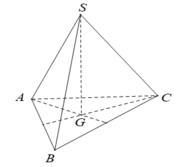
Cách 1:
- Ta có: SA = SB = SC nên:
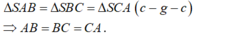
- Do đó, tam giác ABC đều. Gọi G là trọng tâm của tam giác ABC.
- Vì hình chóp S.ABC có SA = SB = SC nên hình chiếu của S trùng với G. Hay SG ⊥ (ABC).
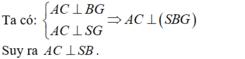
- Vậy góc giữa cặp vectơ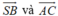 
bằng 90°.
Cách 2:
- Ta có:
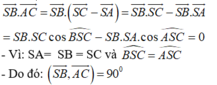
a có \(\angle \left(\right. S C , \left(\right. A B C D \left.\right) \left.\right) = 45^{\circ}\).
Nghĩa là hình chiếu của \(S\) xuống đáy nằm trên đường chéo \(B D\).
Xét tam giác cân \(S A B\), do tính đối xứng ⇒ khoảng cách từ \(A\) đến \(\left(\right. S C D \left.\right)\) chính bằng nửa cạnh hình vuông:
\(d\left(\right.A,\left(\right.SCD\left.\right)\left.\right)=\frac{a}{2}\)
Với \(M\) là trung điểm \(S A\), khoảng cách giảm đi một nửa:
\(d\left(\right.M,\left(\right.SCD\left.\right)\left.\right)=\frac{a}{4}\)
Đáp số
\(d \left(\right. A , \left(\right. S C D \left.\right) \left.\right) = \frac{a}{2}\)
\(d \left(\right. M , \left(\right. S C D \left.\right) \left.\right) = \frac{a}{4}\)
Bạn coi lại dữ liệu bài toán, vừa thừa vừa thiếu
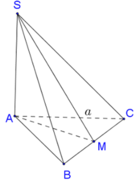
SA=SC=AC nên tam giác SAC đều thì hiển nhiên \(\widehat{CSA}=60^0\) ko cần đề bài phải cho nữa
\(\widehat{ASB}=90^0\) và SA=SB thì tam giác SAB vuông cân tại S nên ta có \(AB=\sqrt{SA^2+SB^2}=a\sqrt{2}\) cũng không cần đề phải cho
Nhưng hoàn toàn ko có dữ liệu BC hoặc góc A của tam giác ABC để định dạng đáy
Chọn D.
Cách 1:
- Ta có: SA = SB = SC nên:
- Do đó, tam giác ABC đều. Gọi G là trọng tâm của tam giác ABC.
- Vì hình chóp S.ABC có SA = SB = SC nên hình chiếu của S trùng với G. Hay SG ⊥ (ABC).
- Vậy góc giữa cặp vectơ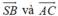
bằng 90°.
Cách 2:
- Ta có: