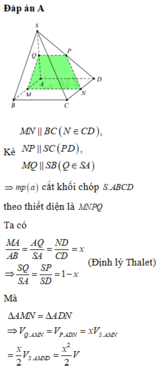
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
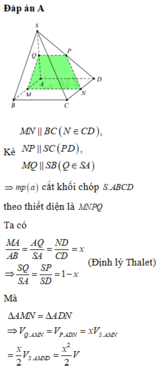
bn ơi K thuộc SD hả ? ... nếu vậy thì MK sẽ không thể song song với mặt phẳng ( SBC) đâu nhé :)
a) () // (ABCD) =>
// AB =>
là trung điểm của SB. Chứng minh tương tự với các điểm còn lại
b) Áp dụng định lí Ta-lét trong không gian:
\(\dfrac{A_1A_2}{A_2A}=\dfrac{B_1B_2}{B_2B}=\dfrac{C_1C_2}{CC_2}=\dfrac{D_1D_2}{D_2D}\).
Do \(A_1A_2=A_2A\) nên : \(\dfrac{A_1A_2}{A_2A}=\dfrac{B_1B_2}{B_2B}=\dfrac{C_1C_2}{CC_2}=\dfrac{D_1D_2}{D_2D}=1\).
Nên \(B_1B_2=B_2B;C_1C_2=CC_2=D_1D_2=D_2D\).
c) Có hai hình chóp cụt:
A B C D M N P Q
a/ Trong mp (BCD) dựng đường thẳng // với CD cắt BD tại P => CD//NP (1)
=> mp (MNP) là mp \(\alpha\)
Trong mp (ACD) từ M dựng đường thẳng //CD cắt AC tại Q => CD//MQ (2)
Từ (1) và (2) => NP//MQ => MPNQ là thiết diện của tứ diện ABCD với mp \(\alpha\)
b/
Xét tg ACD có
MQ//CD và MA=MD => QA=QC (trong tam giác đường thẳng đi qua trung điểm của 1 cạnh và // với 1 cạnh thì đi qua trung điểm cạnh còn lại của tam giác => MQ là đường trung bình của tg ACD \(\Rightarrow MQ=\frac{CD}{2}\)
Ta có MQ//NP để MPNQ là hình bình hành thì \(MQ=NP=\frac{CD}{2}\) (tứ giác có 1 cặp cạnh đối // và = nhau thì tứ giác là hbh)
=> NP là đường trung bình của tg BCD => N là trung điểm của BC
Mình sẽ tóm tắt và giải từng ý nhé.
Đề cho: Hình chóp S.ABCD, đáy ABCD là tứ giác.
M nằm trong tam giác SBC, N nằm trong tam giác SCD.
a) Giao tuyến của (AMN) và (ABCD)
b) Giao điểm của MN với (SAC)
c) Giao điểm của SC với (AMN)
Tóm lại:
a) AI (I là MN ∩ BD)
b) P = MN ∩ (SAC) (thường là trên SC)
c) Cùng điểm P đó
Nếu bạn muốn mình vẽ hình minh họa để nhìn rõ hơn mình có thể làm ngay.
Cho mình xin 1 tick với ạ
