Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Cho tứ diện ABCD có I và J lần lượt là trọng tâm các tam giác ABC và ABD. Chứng minh rằng: IJ // CD.
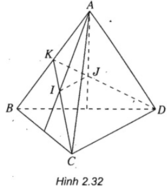
Gọi K là trung điểm của AB.
Vì I là trọng tâm của tam giác ABC nên I ∈ KC và vì J là trọng tâm của tam giác ABD nên J ∈ KD.
Từ đó suy ra
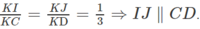
Câu b đề bài thiếu, tìm giao tuyến của mặt nào và (ABD) vậy em?
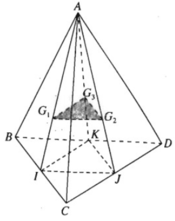
Gọi I, J và K lần lượt là trung điểm của các cạnh BC, CD và BD. Theo tính chất trọng tâm của tam giác ta có:
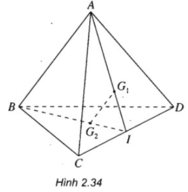
a: Gọi giao điểm của AG với BC là E
Xét ΔABD có
G là trọng tâm
E là giao điểm của AG với BD
Do đó: E là trung điểm của BD và AG=2/3AE
Xét ΔAHD có \(\dfrac{AG}{AE}=\dfrac{AM}{AD}=\dfrac{2}{3}\)
nên GM//ED
=>GM//BD
mà BD\(\subset\left(BCD\right)\) và GM không thuộc mp(BCD)
nên GM//(BCD)
b: Gọi giao của AH với BC là F
Xét ΔABC có
H là trọng tâm
F là giao điểm của AH với BC
Do đó: F là trung điểm của BC và AH=2/3AF
Xét ΔAGE có \(\dfrac{AH}{AF}=\dfrac{AG}{AE}=\dfrac{2}{3}\)
nên HG//FE
mà \(FE\subset\left(BCD\right)\);HG không thuộc(BCD)
nên HG//(BCD)
Gọi I là trung điểm của CD.
Vì G 1 là trọng tâm của tam giác ACD nên G 1 ∈ A I
Vì G 2 là trọng tâm của tam giác BCD nên G 2 ∈ B I
Ta có :
A B ⊂ ( A B C ) ⇒ G 1 G 2 / / ( A B C )
Và A B ⊂ ( A B D ) ⇒ G 1 G 2 / / ( A B D )
Trong mp(ABD), Gọi K là giao điểm của BN và AD
Xét ΔBAD có
N là trọng tâm
K là giao điểm của BN và AD
DO đó: K là trung điểm của AD
Xét ΔBAD có
N là trọng tâm
BK là đường trung tuyến
Do đó: \(BN=\frac23BK\)
Ta có: SM+MB=SB
=>MB=SB-SM=3SM-SM=2SM
=>\(\frac{BM}{BS}=\frac{2MS}{3MS}=\frac23\)
Xét ΔBKS có \(\frac{BN}{BK}=\frac{BM}{BS}\left(=\frac23\right)\)
nên MN//SK
mà SK⊂(SAD) và MN không thuộc mp(SAD)
nên MN//(SAD)
Trong mp(SDC), gọi F là giao điểm của CG và SD
Xét ΔSDC có
G là trọng tâm
F là giao điểm của CG và SD
Do đó: F là trung điểm của SD
Xét ΔSCD có
F là trung điểm của SD
G là trọng tâm
Do đó: \(CG=\frac23CF\)
=>CG=2GF
Trong mp(ABCD), gọi O là giao điểm của AC và BD
ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm chung của AC và BD
Xét ΔDAB có
N là trọng tâm
O là trung điểm của BD
Do đó: A,N,O thẳng hàng
=>\(AN=\frac23AO=\frac23OC;ON=\frac13OA=\frac13OC\)
Vì A,N,O thẳng hàng
và A,O,C thẳng hàng
nên A,N,O,C thẳng hàng
\(NC=NO+OC\)
\(=\frac13AO+AO=\frac43AO\)
=>\(\frac{CN}{NA}=\frac{\frac43AO}{\frac23AO}=\frac43:\frac23=2\)
Xét ΔCAF có \(\frac{CN}{NA}=\frac{CG}{GF}\left(=2\right)\)
nên GN//AF
mà AF⊂(SAD)
và GN không thuộc mp(SAD)
nên GN//(SAD)
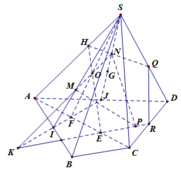
Trong mp(SDA), gọi E là giao điểm của SG với AD
Trong mp(SBC), gọi K là giao điểm của SH với BC
Xét ΔSAD có
G là trọng tâm của ΔSAD
E là giao điểm của SG với AD
Do đó: E là trung điểm của AD
Xét ΔSBC có
H là trọng tâm của ΔSBC
SH cắt BC tại K
Do đó: K là trung điểm của BC
Xét hình thang ABCD(AB//CD) có
E,K lần lượt là trung điểm của AD,BC
=>EK là đường trung bình
=>EK//AB
Xét ΔSDE có
SE là đường trung tuyến
G là trọng tâm
Do đó: \(\dfrac{SG}{SE}=\dfrac{2}{3}\)
Xét ΔSBC có
H là trọng tâm của ΔSBC
SK là đường trung tuyến
Do đó: \(\dfrac{SH}{SK}=\dfrac{2}{3}\)
Xét ΔSEK có \(\dfrac{SG}{SE}=\dfrac{SH}{SK}\left(=\dfrac{2}{3}\right)\)
nên GH//EK
mà EK//AB
nên GH//AB
Ta có: GH//AB
AB\(\subset\)(SAB)
GH không nằm trong mp(SAB)
Do đó: GH//(SAB)
IJ ⊂⊂ (CIJ).
"Mở rộng" mặt phẳng (CIJ) thành (CMN).
Trong tam giác CMN:
CICM=CJCN=23CMCI=CNCJ=32(Do I, J lần lượt là trọng tâm tam giác ADC và tam giác BCD. )
⇒⇒ IJ//MN (Định lý Ta-lét).
Mà MN ⊂⊂ (ABD).
Vậy IJ//(ABD).