Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Gọi H là giao của PN và BC, I là giao của MP và BC
Ta có \(\frac{AN}{AC}+\frac{NC}{AC}=1\left(1\right)\)
Mặt khác áp dụng định lý Talet ta có:
\(\frac{NC}{AC}=\frac{CH}{BC}=\frac{CI+CH}{BC}=\frac{CI}{BC}+\frac{CH}{BC}\left(2\right)\)
Vì MI//AC nên \(\frac{CI}{BC}=\frac{AM}{AB}\left(3\right)\)
Vì \(\Delta\)ABC đồng dạng với \(\Delta\)PHI (gg)
=> \(\frac{IH}{BC}=\frac{PH}{AB}\)mà \(\frac{PH}{AB}=\frac{PQ}{AQ}\left(4\right)\)
Từ (1)(2)(3)(4) => \(\frac{AN}{AC}+\frac{NC}{AC}=....=\frac{AM}{AB}+\frac{AN}{AC}+\frac{PQ}{AQ}=1\left(đpcm\right)\)
b) Từ câu (a) ta có:
\(\frac{AM\cdot AN\cdot PQ}{AB\cdot AC\cdot AQ}=\frac{CI\cdot AN\cdot IH}{BC\cdot AC\cdot BC}=\frac{CI\cdot BH\cdot IH}{BC\cdot BC\cdot BC}=\frac{1}{27}\)
=> \(CI\cdot BH\cdot IH=\frac{BC^3}{27}\)
Mặt khác áp dụng BĐT Cosi cho 3 số không âm ta có:
\(CI\cdot BH\cdot IH\le\frac{\left(CI+IH+HB\right)^3}{3^3}=\frac{1}{27}\)
A B C H Q I P M N
Gọi H = PN ∩ BC; I = MP ∩ BC
a, Ta có: \(\frac{AN}{AC}+\frac{NC}{AC}=1\left(1\right)\)
Mặt khác, áp dụng định lý Ta-lét, ta có:
\(\frac{NC}{AC}=\frac{CH}{BC}=\frac{CI+HI}{BC}=\frac{CI}{BC}+\frac{HI}{BC}\left(2\right)\)
Vì MI//AC nên \(\frac{CI}{BC}=\frac{AM}{AB}\left(3\right)\)
Vì ΔABC đồng dạng với ΔPHI (g.g)
=> \(\frac{HI}{BC}=\frac{PH}{AB}\) mà \(\frac{PH}{AB}=\frac{PQ}{AB}\)
nên \(\frac{HI}{BC}=\frac{PQ}{AB}\left(4\right)\)
Từ (1), (2), (3), (4) suy ra:
\(\frac{AN}{AC}+\frac{NC}{AC}=\frac{AN}{AC}+\frac{CI}{BC}+\frac{HI}{BC}\)
\(=\frac{AN}{AC}+\frac{AM}{AB}+\frac{PQ}{AQ}=1\left(đpcm\right)\)
b, Từ câu a ta có:
\(\frac{AM.AN.PQ}{AB.AC.AQ}=\frac{CI.AN.IH}{BC.AC.BC}=\frac{CI.BH.IH}{BC.BC.BC}=\frac{1}{27}\)
\(\Leftrightarrow CI.BH.IH=\frac{1}{27}.BC^3\)
Áp dụng BĐT Cô-si cho 3 số không âm, ta có:
\(CI.BH.IH\le\frac{\left(CI+BH+IH\right)^3}{3^3}=\frac{1}{27}.BC^3\)
Dấu "=" xảy ra <=> CI = BH = IH
<=> Q là trung điểm của BC và AP\(=\frac{2}{3}AQ\)

Đề bài:
Cho \(A M\), \(A N\) là tiếp tuyến của (O), \(M I\) là đường kính của (O). Gọi \(P\) là trung điểm của \(A O\). \(M P\) cắt \(N I\) tại \(E\).
- Chứng minh rằng \(A E O M\) là hình bình hành.
- Tiếp tuyến tại \(I\) của (O) cắt \(M N\) tại \(K\). Chứng minh rằng \(A I \bot O K\).
Giải quyết bài toán:
1. Chứng minh rằng \(A E O M\) là hình bình hành.
1.1. Các tính chất quan trọng
- \(A M\) và \(A N\) là các tiếp tuyến từ điểm \(A\) đến đường tròn \(\left(\right. O \left.\right)\), vì vậy ta có:
\(A M = A N (\text{c} \overset{ˊ}{\text{a}} \text{c}\&\text{nbsp};\text{ti} \overset{ˊ}{\hat{\text{e}}} \text{p}\&\text{nbsp};\text{tuy} \overset{ˊ}{\hat{\text{e}}} \text{n}\&\text{nbsp};\text{t}ừ\&\text{nbsp};\text{c} \overset{ˋ}{\text{u}} \text{ng}\&\text{nbsp};\text{m}ộ\text{t}\&\text{nbsp};đ\text{i}ể\text{m}\&\text{nbsp};đ \overset{ˊ}{\hat{\text{e}}} \text{n}\&\text{nbsp};đườ\text{ng}\&\text{nbsp};\text{tr} \overset{ˋ}{\text{o}} \text{n}) .\)
Hơn nữa, tiếp tuyến vuông góc với bán kính tại điểm tiếp xúc, do đó:
\(A M \bot O M \text{v} \overset{ˋ}{\text{a}} A N \bot O N .\) - \(M I\) là đường kính của đường tròn \(\left(\right. O \left.\right)\), do đó \(O M = O I\).
- \(P\) là trung điểm của \(A O\), do đó:
\(A P = P O .\)
1.2. Chứng minh rằng \(A E O M\) là hình bình hành
Để chứng minh \(A E O M\) là hình bình hành, ta cần chứng minh rằng hai cặp cạnh đối diện của tứ giác này song song và bằng nhau.
- Cặp 1: \(A E \parallel O M\)
Ta đã biết rằng \(M P\) cắt \(N I\) tại \(E\), và \(P\) là trung điểm của \(A O\), do đó, ta có thể sử dụng tính chất của các đường chéo cắt nhau tại trung điểm để chứng minh \(A E \parallel O M\). Điều này là do \(M P\) và \(N I\) là các đường chéo của các tam giác đồng dạng, và sự cắt nhau tại \(P\) tạo ra mối quan hệ song song giữa \(A E\) và \(O M\). - Cặp 2: \(A M \parallel E O\)
Xét \(\triangle A M O\) và \(\triangle E O M\). Ta có \(A M = E O\) (vì \(A M = A N\) và \(A N = E O\)do \(A M\) là tiếp tuyến và \(O I = O M\)). Hơn nữa, góc \(\angle A M O = \angle E O M\) vì chúng là góc đối đỉnh. Do đó, theo định lý đồng dạng, ta có:
\(A M \parallel E O .\)
Vì vậy, ta đã chứng minh được rằng \(A E O M\) là hình bình hành.
2. Chứng minh rằng \(A I \bot O K\).
2.1. Tiếp tuyến tại \(I\) của (O) cắt \(M N\) tại \(K\)
- Tiếp tuyến tại điểm \(I\) vuông góc với bán kính \(O I\) tại \(I\), tức là:
\(A I \bot O I .\) - Tiếp tuyến này cắt \(M N\) tại điểm \(K\), và ta cần chứng minh rằng \(A I \bot O K\).
2.2. Sử dụng tính chất của tiếp tuyến
- Tính chất tiếp tuyến chỉ ra rằng tiếp tuyến tại \(I\) của đường tròn \(\left(\right. O \left.\right)\) vuông góc với bán kính \(O I\).
- Khi tiếp tuyến này cắt \(M N\) tại \(K\), ta có thể xem \(\triangle A O K\) và \(\triangle A I K\) trong đó góc \(\angle A I K\) là góc vuông. Ta cần chứng minh rằng góc này thực sự là góc vuông.
2.3. Góc vuông giữa \(A I\) và \(O K\)
- Xét các tam giác vuông \(\triangle A I K\) và \(\triangle O K I\), ta có:
\(\angle A I K = 90^{\circ} (\text{do}\&\text{nbsp};\text{t} \overset{ˊ}{\imath} \text{nh}\&\text{nbsp};\text{ch} \overset{ˊ}{\hat{\text{a}}} \text{t}\&\text{nbsp};\text{c}ủ\text{a}\&\text{nbsp};\text{ti} \overset{ˊ}{\hat{\text{e}}} \text{p}\&\text{nbsp};\text{tuy} \overset{ˊ}{\hat{\text{e}}} \text{n}) .\)
Do đó, \(A I \bot O K\), vì \(A I\) là tiếp tuyến tại \(I\) và \(O K\) là tiếp tuyến tại \(K\).
Kết luận:
- AEOM là hình bình hành: Dựa vào các tính chất của tiếp tuyến và đoạn cắt nhau, ta đã chứng minh được rằng \(A E O M\) là hình bình hành.
- AI vuông góc với OK: Sử dụng tính chất của tiếp tuyến tại \(I\) và các tam giác vuông, ta đã chứng minh được rằng \(A I \bot O K\).

Bài toán: Cho AM, AN là tiếp tuyến của (O), MI là đường kính của (O). Gọi P là trung điểm của AO. MP cắt NI tại E.
- Chứng minh rằng AEOM là hình bình hành.
- Tiếp tuyến tại I của (O) cắt MN tại K. Chứng minh rằng AI vuông góc với OK.
Giải pháp bài 1: Chứng minh AEOM là hình bình hành
1.1. Sử dụng tính chất của tiếp tuyến
- Ta biết rằng \(A M\) và \(A N\) là hai tiếp tuyến từ điểm \(A\) đến đường tròn (O).
- Theo tính chất của tiếp tuyến, ta có:
\(A M = A N (\text{c} \overset{ˋ}{\text{u}} \text{ng}\&\text{nbsp};\text{chi} \overset{ˋ}{\hat{\text{e}}} \text{u}\&\text{nbsp};\text{d} \overset{ˋ}{\text{a}} \text{i}\&\text{nbsp};\text{ti} \overset{ˊ}{\hat{\text{e}}} \text{p}\&\text{nbsp};\text{tuy} \overset{ˊ}{\hat{\text{e}}} \text{n}\&\text{nbsp};\text{t}ừ\&\text{nbsp};\text{A}\&\text{nbsp};đ \overset{ˊ}{\hat{\text{e}}} \text{n}\&\text{nbsp};(\text{O}))\)
và các đoạn \(A M \bot O M\) và \(A N \bot O N\) (tiếp tuyến vuông góc với bán kính tại điểm tiếp xúc).
1.2. Tính chất của trung điểm P
- \(P\) là trung điểm của đoạn \(A O\), nên \(A P = P O\).
1.3. Đoạn \(M P\) và \(N I\) cắt nhau tại \(E\)
- Ta sẽ xét các điểm và quan hệ của đoạn thẳng cắt nhau tại \(E\). Tuy nhiên, để chứng minh \(A E O M\) là hình bình hành, ta cần phải chứng minh rằng:
- \(A E \parallel O M\) và \(A M \parallel E O\).
- Hoặc chứng minh \(A E = O M\) và \(A M = E O\).
1.4. Các bước tiếp theo
Vì chưa có đủ thông tin chi tiết về vị trí điểm \(E\), chúng ta cần sử dụng các định lý về tứ giác trong hình học phẳng, đặc biệt là việc áp dụng định lý về hình bình hành.
Giải pháp bài 2: Chứng minh rằng AI vuông góc với OK
2.1. Tiếp tuyến tại I của (O)
- Ta biết tiếp tuyến tại \(I\) của đường tròn (O) cắt \(M N\) tại điểm \(K\).
- Theo tính chất của tiếp tuyến, \(M I \bot I O\).
2.2. Góc vuông giữa AI và OK
- Để chứng minh \(A I \bot O K\), ta cần tìm ra mối quan hệ giữa các đoạn thẳng trong tam giác hoặc tứ giác có chứa điểm \(K\).
- Mối quan hệ này có thể sử dụng các định lý về góc vuông và tiếp tuyến, chẳng hạn như việc tiếp tuyến vuông góc với bán kính tại điểm tiếp xúc. Khi đó, \(A I\) và \(O K\) sẽ vuông góc với nhau.
Kết luận:
- Việc chứng minh \(A E O M\) là hình bình hành đòi hỏi chúng ta phải có thêm các thông tin về các điểm cắt và các tính chất của các đoạn thẳng, ví dụ như \(A E \parallel O M\) hoặc \(A M = E O\).
- Việc chứng minh \(A I \bot O K\) có thể được thực hiện bằng cách sử dụng tính chất của tiếp tuyến và các góc vuông tại điểm tiếp xúc của tiếp tuyến.

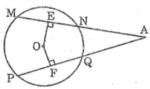
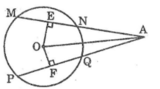
Nối OA
Ta có: MN = PQ (gt)
Suy ra: OE = OF (hai dây bằng nhau cách đều tâm)
Xét hai tam giác OAE và OAF, ta có:
![]()
OA chung
OE = OF (chứng minh trên)
Suy ra: ΔOAE = ΔOAF (cạnh huyền, cạnh góc vuông)
Suy ra: AE = AF
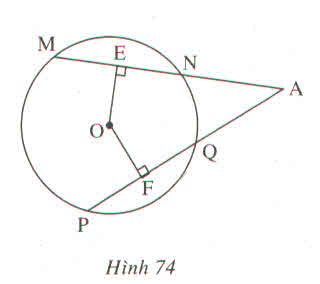

Ta có: OE ⊥ MN (gt)
Suy ra EN = (1/2).MN (đường kính vuông góc với dây cung) (1)
OF ⊥ PQ (gt)
Suy ra FQ = (1/2).PQ (đường kính vuông góc với dây cung) (2)
Mặt khác: MN = PQ (gt) (3)
Từ (1), (2) và (3) suy ra: EN = FQ (4)
Mà AE = QF (chứng minh trên) (5)
Từ (4) và (5) suy ra: AN + NE = AQ + QF (6)
Từ (5) và (6) suy ra: AN = AQ