Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

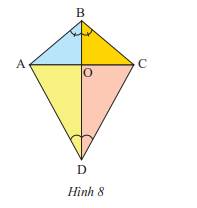
a) Tia BO là tia phân giác của \(\widehat {ABC}\) vì tia BO nằm giữa 2 tia BA và BC, tạo với 2 cạnh BA và BC 2 góc bằng nhau.
Tia DO là tia phân giác của \(\widehat {ADC}\) vì tia DO nằm giữa 2 tia DA và DC, tạo với 2 cạnh DA và DC 2 góc bằng nhau
b) Vì BO là tia phân giác của \(\widehat {ABC}\) nên \(\widehat {ABO} = \widehat {CBO} = \frac{1}{2}.\widehat {ABC} = \frac{1}{2}.100^\circ = 50^\circ \)
Vì DO là tia phân giác của \(\widehat {ADC}\)nên \(\widehat {ADO} = \widehat {CDO} = \frac{1}{2}.\widehat {ADC} = \frac{1}{2}.60^\circ = 30^\circ \)
Vậy \(\widehat {ABO} = 50^\circ ;\widehat {ADO} = 30^\circ \)

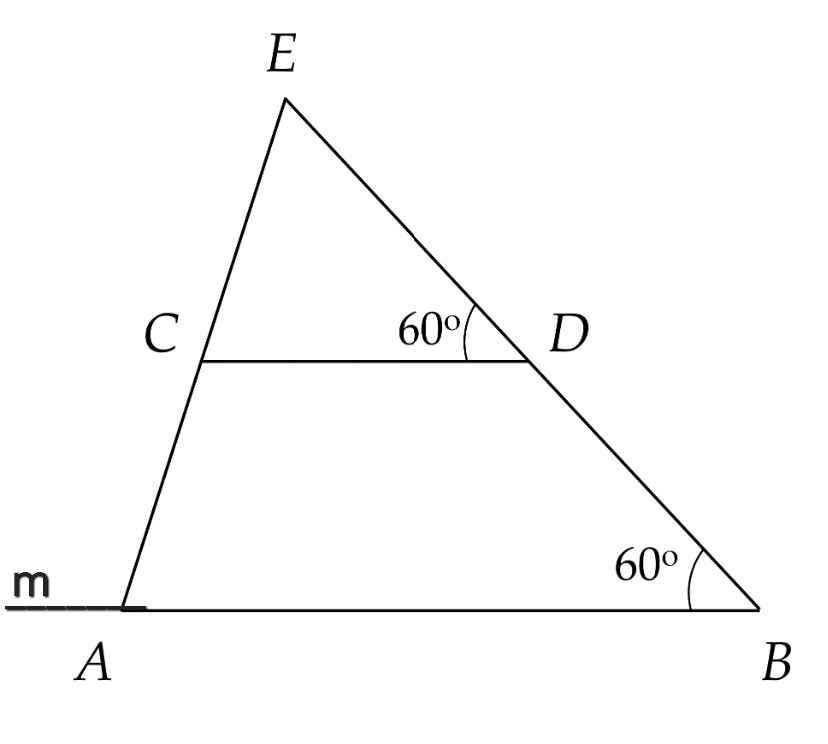
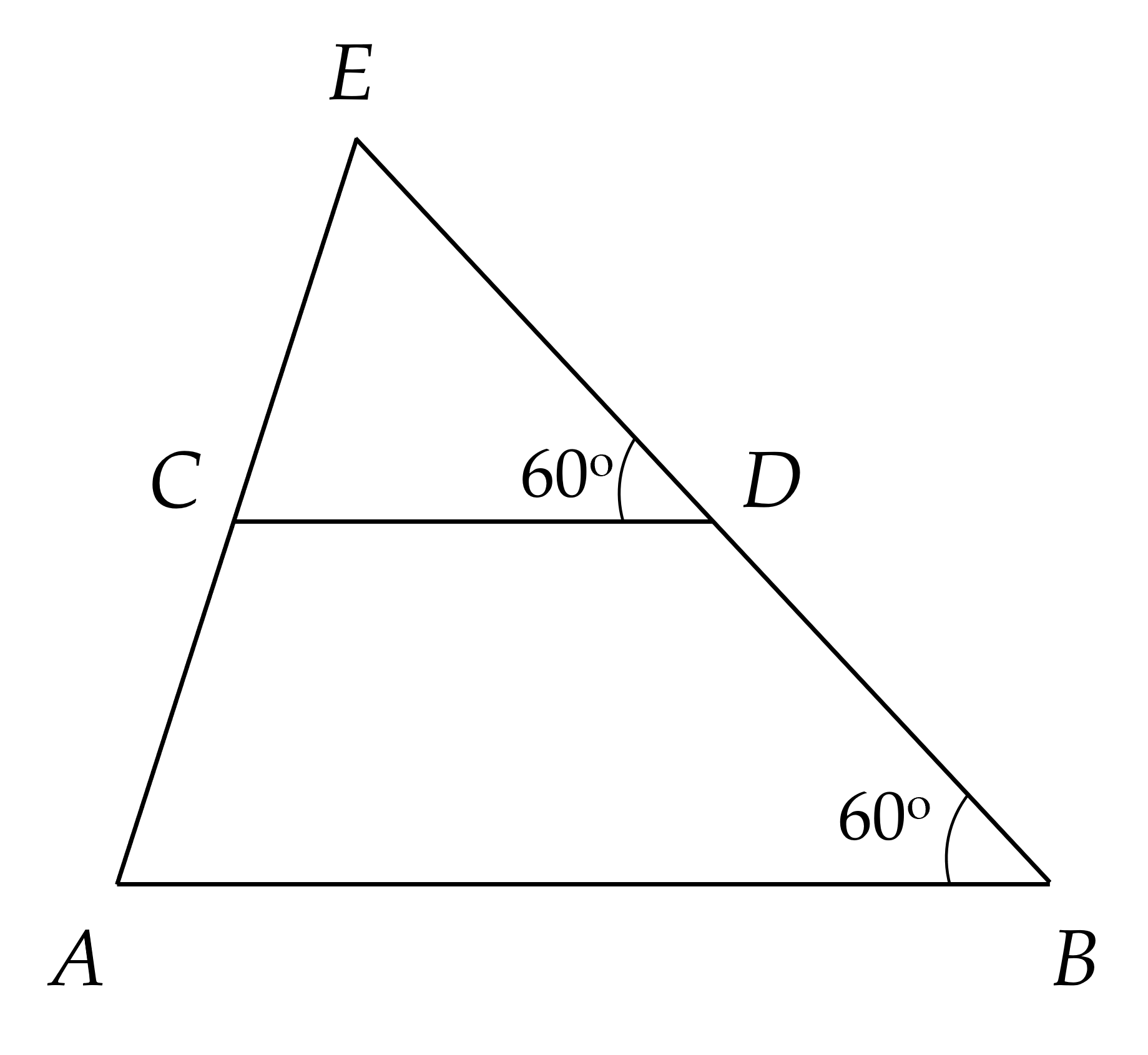
a) Ta có:
∠ABD = ∠CDE = 60⁰ (gt)
Mà ∠ABD và ∠CDE là hai góc so le trong
⇒ AB // CD
b) Vẽ tia Am là tia đối của tia AB
Do AB // CD
⇒ ∠mAC = ∠ACD (so le trong)
Mà ∠mAC + ∠BAC = 180⁰ (kề bù)
⇒ ∠ACD + ∠BAC = 180⁰

a) Ta có:
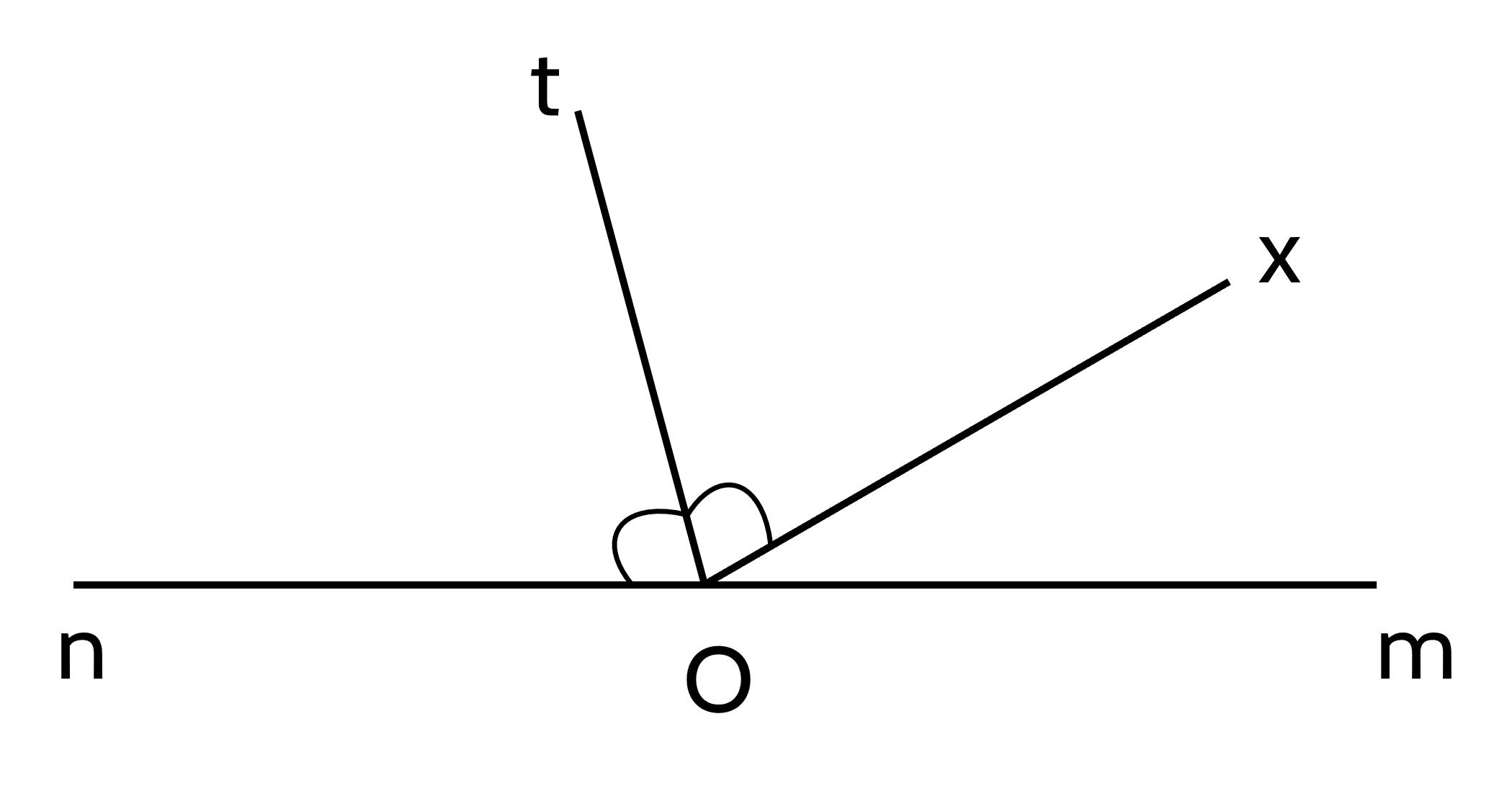
∠mOx + ∠nOx = 180⁰ (kề bù)
⇒ ∠nOx = 180⁰ - ∠mOx
= 180⁰ - 30⁰
= 150⁰
Do Ot là tia phân giác của ∠nOx
⇒ ∠nOt = ∠nOx : 2
= 150⁰ : 2
= 75⁰
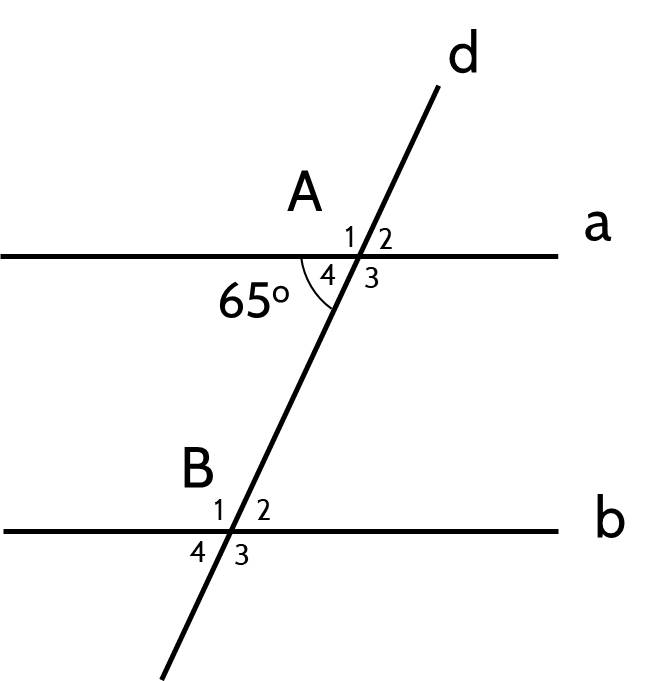
b) Do a // b
⇒ ∠B₄ = ∠A₄ = 65⁰ (đồng vị)
Ta có:
∠B₃ + ∠B₄ = 180⁰ (kề bù)
⇒ ∠B₃ = 180⁰ - ∠B₄
= 180⁰ - 65⁰
= 115⁰
Tính số đo góc �3^B3.
Hướng dẫn giải:a) ���^+���^=180∘mOx+xOn=180∘
Vậy ���^=180∘−30∘=150∘nOx=180∘−30∘=150∘.
��Ot là tia phân giác của ���^nOx, suy ra ���^=12.���^=75∘nOt=21.nOx=75∘.
b) a // b suy ra �4^=�2^=65∘A4=B2=65

a/
\(Ax\perp m\left(gt\right);By\perp m\left(gt\right)\) => Ax//By (cùng vuông góc với m)
Mà Cz//Ax (gt)
=> Cz//By (cùng // với Ax)
b/
\(\widehat{BCz}=\widehat{ACB}-\widehat{C}=110^o-30^o=80^o\)
Ta có
Cz//By (cmt) \(\Rightarrow\widehat{BCz}=\widehat{CBy}=80^o\) (góc so le trong)
c/
\(CD\perp Ax\left(gt\right)\Rightarrow\widehat{ADC}=90^o\)
Cz//Ax (gt) \(\Rightarrow\widehat{A}=\widehat{C}=30^o\) (Góc so le trong)
Xét tg vuông ACD có
\(\widehat{ACD}=\widehat{ADC}-\widehat{A}=90^o-30^o=60^o\)

Giải:
Góc xMN = góc MNt = 70\(^0\) (hai góc so le trong)
Suy ra: xy // zt
Góc xMN = Góc mMy = 70\(^0\) (đối đỉnh)
Góc MNt = góc zNn = 70\(^0\) hai góc đối đỉnh
\(\hat{xMN}\) + \(\hat{xMm}\) = 180\(^0\) (hai góc kề bù)
\(\hat{xMm}\) = 180\(^0-70^0=110^0\)
\(\hat{xMm}=\hat{NMy}\) = 110\(^0\) (đối đỉnh)
Góc NMy = góc MNz = 110\(^0\) (so le trong)
Góc MNz = Góc nNt = 110\(^0\) (đối đỉnh)
Ta có: \(\hat{xMN}=\hat{tNM}\left(=70^0\right)\)
mà hai góc này là hai góc ở vị trí so le trong
nên xy//zt
=>\(\hat{yMN}=\hat{zNM}\) (hai góc so le trong)
Ta có: xy//zt
=>\(\hat{xMN}+\hat{zNM}=180^0\) (hai góc trong cùng phía)
=>\(\hat{zNM}=180^0-70^0=110^0\)
Ta có: \(\hat{zNM}=\hat{yMN}\) (cmt)
mà \(\hat{zNM}=110^0\)
nên \(\hat{yMN}=110^0\)
Các cặp góc đồng vị là: \(\hat{yMm};\hat{tNM}\) ; \(\hat{xMm};\hat{zNM}\) ; \(\hat{xMN};\hat{zNn}\) ; \(\hat{yMN};\hat{tNn}\)
Ta có: \(\hat{xMN}=\hat{mMy}\) (hai góc đối đỉnh)
mà \(\hat{xMN}=70^0\)
nên \(\hat{mMy}=70^0\)
Ta có: \(\hat{yMN}=\hat{xMm}\) (hai góc đối đỉnh)
mà \(\hat{yMN}=110^0\)
nên \(\hat{xMm}=110^0\)
Ta có: \(\hat{MNt}=\hat{zNn}\) (hai góc đối đỉnh)
mà \(\hat{MNt}=70^0\)
nên \(\hat{zNn}=70^0\)
Ta có: \(\hat{zNM}=\hat{tNn}\) (hai góc đối đỉnh)
mà \(\hat{zNM}=110^0\)
nên \(\hat{tNn}=110^0\)

Bài 4:
\(\frac{2^8.9^5}{6^9}\)
= \(\frac{2^8.\left(3^2\right)^5}{\left(2.3\right)^9}\)
= \(\frac{2^8.3^{10}}{2^9.3^9}\)
= \(\frac32\)
Câu 6:
\(\frac{6^{25}}{4^{12}\times9^{13}}\)
= \(\frac{\left(2.3\right)^{25}}{\left(2^2\right)^{12}.\left(3^2\right)^{13}}\)
= \(\frac{2^{25}\times3^{25}}{2^{24}\times3^{26}}\)
= \(\frac23\)

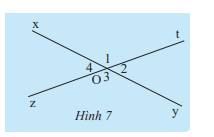
\(\widehat {{O_1}}\) có cạnh Ox và Ot, đỉnh O
\(\widehat {{O_3}}\) có cạnh Oy và Oz, đỉnh O
Ta có: \(\widehat {{O_1}}\) và \(\widehat {{O_3}}\) có mỗi cạnh của góc này là cạnh đối của một cạnh của góc kia.
\(\widehat {{O_1}}\) và \(\widehat {{O_3}}\) có chung đỉnh

Xét 2 tam giác ABC và MNP có:
AB=MN (gt)
\(\widehat {BAC} = \widehat {NMP}\) (gt)
AC=MP (gt)
Vậy \(\Delta ABC = \Delta MNP\)(c.g.c)
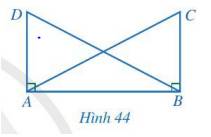




Xét hai tam giác vuông DAB và CBA: AC = BD; AB chung.
Nên \(\Delta DAB = \Delta CBA\) (cạnh huyền - cạnh góc vuông)
Nên AD = BC ( 2 cạnh tương ứng)