Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Nếu HB = HC ⇒ HB2 = HC2.
⇒ AH2 + HB2 = AH2 + HC2
Kết hợp với 2 điều kiện (1) và (2)
⇒ AB2 = AC2
⇒ AB = AC
- Nếu AB = AC ⇒ AB2 = AC2
Kết hợp với 2 điều kiện (1) và (2)
⇒ AH2 + HB2 = AH2 + HC2
⇒ HB2 = HC2
⇒ HB = HC

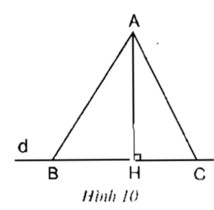
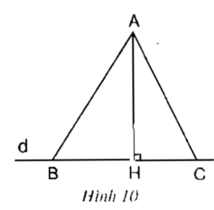
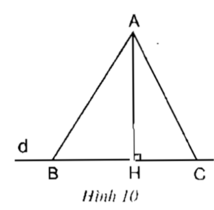
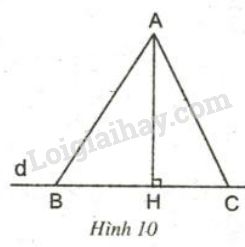
Xét tam giác AHB vuông tại H
Áp dụng định lí Py-ta-go ta có:
AB2 = AH2 + HB2 (1)
Xét tam giác AHC vuông tại H
Áp dụng định lí Py-ta-go ta có:
AC2 = AH2 + HC2 (2)
Nếu HB > HC ⇒ HB2 > HC2.
⇒ AH2 + HB2 > AH2 + HC2
Kết hợp với 2 điều kiện (1) và (2)
⇒ AB2 > AC2
⇒ AB > AC

\(\frac{2}{4}=\frac{3}{6}=\frac{2+3}{4+6}\)
\(\frac{2}{4}=\frac{3}{6}=\frac{2-3}{4-6}\)
\(\Rightarrow\frac{2+3}{4+6}=\frac{2-3}{4-6}\)

A B C D H E I
Lấy E đối xứng với D qua AB, ED cắt AB tại I
Vì AD là phân giác \(\widehat{BAC}\)\(\Rightarrow\frac{BD}{CD}=\frac{AB}{AC}< 1\)
\(\Rightarrow BD< CD\)
\(\Rightarrow BC>2BD\)
Vì DI // CH
\(\Rightarrow\frac{DI}{CH}=\frac{BD}{BC}< \frac{1}{2}\)
\(\Rightarrow CH>2DI=DE\left(1\right)\)
Xét \(\Delta ABC\)ta có: \(AB< AC< BC\)
\(\Rightarrow\widehat{ACB}< \widehat{ABC}< \widehat{BAC}\)
\(\Rightarrow2\widehat{BAC}>\widehat{ACB}+\widehat{ABC}\)
\(\Rightarrow\widehat{BAC}>\frac{\widehat{ACB}+\widehat{ABC}}{2}=\frac{180^o-\widehat{BAC}}{2}\)
Xét \(\Delta AED\)ta có:
\(\widehat{AED}=\widehat{ADE}=\frac{180^o-\widehat{EAD}}{2}=\frac{180^o-\widehat{BAC}}{2}< \widehat{BAC}=\widehat{EAD}\)
\(\Rightarrow ED>AE=AD\left(2\right)\)
Từ (1) và (2) \(\Rightarrow CH>AD\)
mk mới học lớp 5 nên ko biết, mong bạn thông cảm, chúc bạn học giỏi nha

Bài này không chứng minh được theo kiến thức lớp 6, 7 và tiểu học. Phải áp dụng tam giác đồng dạng của lớp 8.
Hoàng Tuấn Đăng A hai à, thầy em bảo làm theo cách tiểu học, cách tính S tam giác + lớp 6,7 đó a ạ

a: Gọi D là giao điểm của BM và AC
Xét ΔABD có AB+AD>BD
=>AB+AD>BM+MD
Xét ΔMDC có MD+DC>MC
Do đó; AB+AD+MD+DC>BM+MD+MC
=>AB+AC+MD>BM+MC+MD
=>AB+AC>BM+MC
b: Gọi E,F lần lượt là giao điểm của MN với AB và AC
Xét ΔBEM có BM<BE+EM
Xét ΔCFN có CN<CF+FN
Xét ΔAEF có EF<AE+AF
Ta có: BM<BE+EM
CN<CF+FN
Do đó: BM+CN<BE+EM+CF+FN
=>BE+EM+CF+FN>BM+CN
=>BE+EM+CF+FN+MN>BM+CN+MN
=>BE+CF+EF>BM+CN+MN
=>BM+CN+MN<BE+CF+EF
mà BE+CF+EF<BE+CF+AE+AF=(BE+AE)+(AF+AC)=AB+AC
nên BM+CN+MN<AB+AC
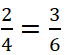
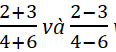 với các tỉ số trong tỉ lệ thức đã cho.
với các tỉ số trong tỉ lệ thức đã cho.


AB > AC ⇒ AB2 > AC2
Kết hợp với 2 điều kiện (1) và (2)
⇒ AH2 + HB2 > AH2 + HC2
⇒ HB2 > HC2
⇒ HB > HC