Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) Điểm (-1 ; 1) thuộc đồ thị của hàm số ⇔ .
b) m = 1 . Tập xác định : R.
y' = 0 ⇔ x = 0.
Bảng biến thiên:
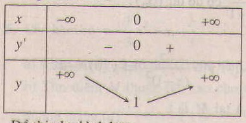
Đồ thị như hình bên.
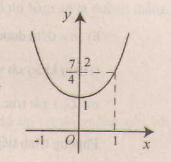
c) Vậy hai điểm thuộc (C) có tung độ
là A(1 ;
) và B(-1 ;
). Ta có y'(-1) = -2, y'(1) = 2.
Phương trình tiếp tuyến với (C) tại A là : y - = y'(1)(x - 1) ⇔ y = 2x -
Phương trình tiếp tuyến với (C) tại B là : y - = y'(-1)(x + 1) ⇔ y = -2x -
.
y = 2x2 + 2mx + m -1 (Cm). Đây là hàm số bậc hai, đồ thị là parabol quay bề lõm lên phía trên.
a) m = 1 ⇒ y = 2x2 + 2x
Tập xác định D = R
\(\lim\limits_{x\rightarrow+\infty}y\left(x\right)=\lim\limits_{x\rightarrow-\infty}=+\infty\)
Bảng biến thiên:
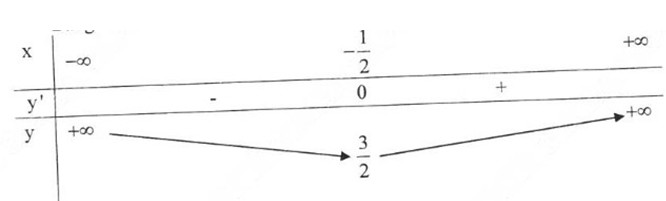
Đồ thị hàm số:
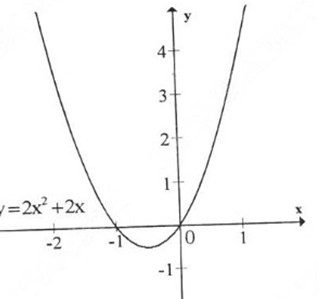
b) Tổng quát y = 2x2 + 2mx + m -1 có tập xác định D = R
y′=4x+2m=0⇔\(x=-\dfrac{m}{2}\).
Suy ra y’ > 0 với \(x>-\dfrac{m}{2}\) và \(y'< 0\) với \(x< -\dfrac{m}{2}\) tức là hàm số nghịch biến trên \(\left(-\infty;\dfrac{-m}{2}\right)\) và đồng biến trên \(\left(-\dfrac{m}{2};+\infty\right)\)
i) Để hàm số đồng biến trên khoảng (-1, +∞) thì phải có điều kiện (−1,+∞)∈(−\(\dfrac{m}{2}\),+∞)
Hay \(-\dfrac{m}{2}< -1\)\(\Leftrightarrow m>2\)
ii) Hàm số đạt cực trị tại \(x=\dfrac{m}{2}\)
Để hàm số đạt cực trị trong khoảng (-1, +∞), ta phải có:
\(-\dfrac{m}{2}\in\left(-1;+\infty\right)\) hay \(-\dfrac{m}{2}>-1\Leftrightarrow m< 2\).
c) (Cm) luôn cắt Ox tại hai điểm phân biệt
⇔ phương trình 2x2 + 2mx + m – 1 = 0 có hai nghiệm phân biệt.
Ta có:
Δ’ = m2 – 2m + 2 = (m-1)2 + 1 > 0 ∀m
Vậy (Cm) luôn cắt O x tại hai điểm phân biệt.
. Tập xác định : R 
{
} ;
và 
;
) ∈ ∆ ⇔ 
.
a) Xét hàm số y = f(x)=12x4−3x2+32f(x)=12x4−3x2+32 (C) có tập xác định: D = R
y’ = 2x3 – 6x = 2x(x2 – 3)
y’ = 0 ⇔ x = 0, x = ±√3
Bảng biến thiên:
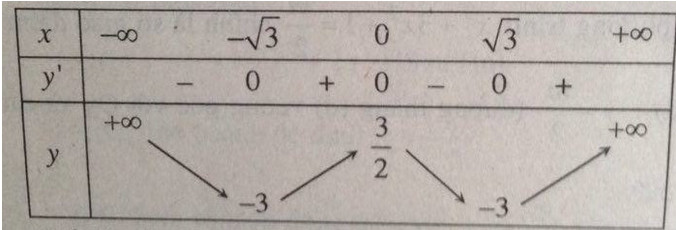
Đồ thị hàm số:
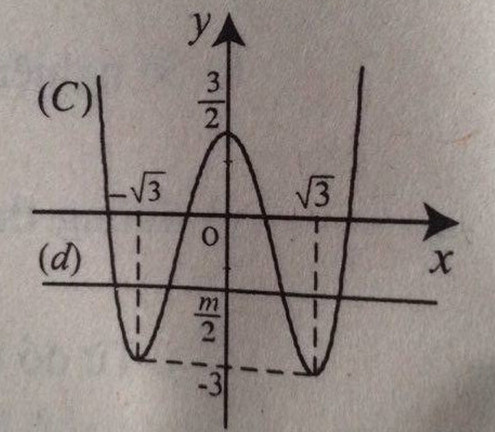
b)
y’’ = 6x2 – 6x
y’’ = 0 ⇔ 6x2 – 6x = 0 ⇔ x = ± 1
y’(-1) = 4, y’’(1) = -4, y(± 1) = -1
Tiếp tuyến của (C) tại điểm (-1, -1) là : y = 4(x+1) – 1= 4x+3
Tiếp tuyến của (C) tại điểm (1, -1) là: y = -4(x-1) – 1 = -4x + 3
c) Ta có: \(x^4-6x^2+3=m\)\(\Leftrightarrow\dfrac{x^4}{2}-3x^2+\dfrac{3}{2}=\dfrac{m}{2}\).
Số nghiệm của (1) là số giao điểm của (C) và đường thẳng (d) : \(y=\dfrac{m}{2}\).
Dễ thấy:
m < -6: ( 1) vô nghiệm
m = -6 : (1) có 2 nghiệm
-6 < m < 3: (1) có 4 nghiệm
m = 3: ( 1) có 3 nghiệm
m > 3: (1) có 2 nghiệm
a) y = x3 + 3x2 + 1
Tập xác định: D = R
y’= 3x2 + 6x = 3x(x+ 2)
y’=0 ⇔ x = 0, x = -2
Bảng biến thiên:
Đồ thị hàm số:
b) Số nghiệm của phương trình \(x^3+3x^2+1=\dfrac{m}{2}\) chính là số giao điểm của (C) và đường thẳng (d): \(y=\dfrac{m}{2}\) (đường thẳng (d) vuông góc với Oy và cắt Oy tại \(\dfrac{m}{2}\) )
Từ đồ thị ta thấy:
- Với \(\dfrac{m}{2}< 1\Leftrightarrow m< 2\) : (d) cắt (C) tại 1 điểm, phương trình có 1 nghiệm
- Với \(\dfrac{m}{2}=1\Leftrightarrow m=2\) : (d) tiếp xúc với (C) tại 1 điểm và cắt (C) tạo 1 điểm, phương trình có hai nghiệm.
- Với \(1< \dfrac{m}{2}< 5\)\(\Leftrightarrow2< m< 10\)
- Với \(\dfrac{m}{2}=5\Leftrightarrow m=10\): (d) cắt (C) tại 1 điểm và tiếp xúc với (C) tại 1 điểm, phương trình có hai nghiệm.
- Với \(\dfrac{m}{2}>5\Leftrightarrow m>10\): (d) cắt (C) tại 1 điểm, phương trình có 1 nghiệm
c) Điểm cực đại (-2, 5), điểm cực tiểu (0, 1).
Đường thẳng đi qua hai điểm này có phương trình là: 1\(y-14=x-2\Leftrightarrow y=x+12\).
a) y = x3 + 3x2 + 1
Tập xác định: D = R
y’= 3x2 + 6x = 3x(x+ 2)
y’=0 ⇔ x = 0, x = -2
Bảng biến thiên:
Đồ thị hàm số:
b) Số nghiệm của phương trình x^3+3x^2+1=m/2chính là số giao điểm của (C) và đường thẳng (d): y=m/2 (đường thẳng (d) vuông góc với Oy và cắt Oy tại )
Từ đồ thị ta thấy:
- Với m/2<1⇔m<2: (d) cắt (C) tại 1 điểm, phương trình có 1 nghiệm
- Với m/2=1⇔ m = 2: (d) tiếp xúc với (C) tại 1 điểm và cắt (C) tạo 1 điểm, phương trình có hai nghiệm
- Với 1<m/2<5⇔ 2<m
- Với m/2=5⇔m=10: (d) cắt (C) tại 1 điểm và tiếp xúc với (C) tại 1 điểm, phương trình có hai nghiệm.
- Với m/2>5⇔m>10 : (d) cắt (C) tại 1 điểm, phương trình có 1 nghiệm
c) Điểm cực đại (-2, 5), điểm cực tiểu (0, 1).
Đường thẳng đi qua hai điểm này có phương trình là: y−14=x−2⇔y=−2x+1
a) Tập xác định : D = R
limx→−∞f(x)=+∞limx→+∞f(x)=−∞y′=−3x2+6x+9=0⇔x=−1,x=3limx→−∞f(x)=+∞limx→+∞f(x)=−∞y′=−3x2+6x+9=0⇔x=−1,x=3
Bảng biến thiên:
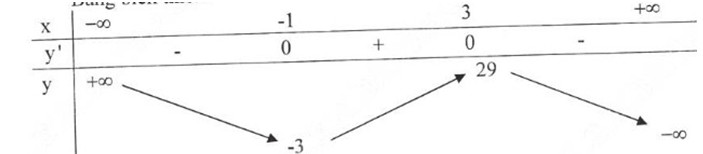
Đồ thị hàm số:
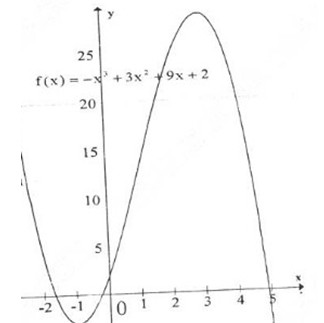
b) y=f(x) = f(x) = -x3+3x2+9x+2.
f’(x) = -3x2+6x+9. Do đó:
f’(x-1)=-3(x-1)2+6(x-1)+9
= -3x2 + 12x = -3x(x-4) > 0 ⇔ 0 < x < 4
c) f’’(x) = -6x+6
f’’(x0) = -6 ⇔ -6x0 + 6 = -6 ⇔ x0 = 2
Do đó: f’(2) = 9, f(2) = 24. Phương trình tiếp tuyến của (C) tại x0 = 2 là:
y=f’(2)(x-2) + f(2) hay y = 9x+6
a) y′=3x+2(m+3)x=x[3x+2(m+3)];y′=0⇔x1=0y′=3x2+2(m+3)x=x[3x+2(m+3)];y′=0⇔x1=0
hoặc x2=−2m+63x2=−2m+63
Xảy ra hai trường hợp đối với dấu của y':
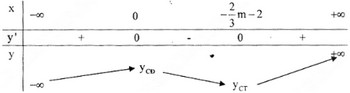
Rõ ràng, để hàm số có điểm cực đại tại x = -1 ta phải có
x2=−2m+63=−1⇔m=−32x2=−2m+63=−1⇔m=−32
(Chú ý : trường hợp x1 = x2 thì hàm số không có cực trị).
b) (Cm) cắt Ox tại x = -2 ⇔ -8 + 4(m + 3) + 1 - m = 0 ⇔ m=−53m=−53
a) y= -x4 + 2mx2 – 2m + 1(Cm). Tập xác định: D = R
y ‘ = -4x3 + 4mx = -4x (x2 – m)
- Với m ≤ 0 thì y’ có một nghiệm x = 0 và đổi dấu + sang – khi qua nghiệm này. Do đó hàm số có một cực đại là x = 0
Do đó, hàm số có 2 cực trị tại x = ± √m và có một cực tiểu tại x = 0
b) Phương trình -x4 + 2mx2 – 2m + 1 = 0 luôn có nghiệm x = ± 1 với mọi m nên (Cm) luôn cắt trục hoành.
c) Theo lời giải câu a, ta thấy ngay:
với m > 0 thì đồ thị (Cm) có cực đại và cực tiểu.
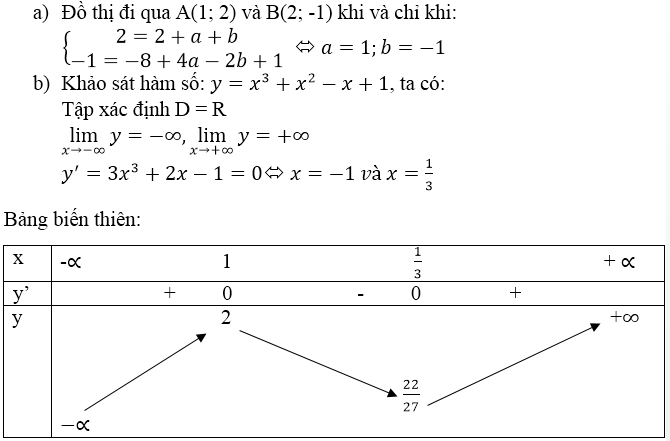
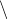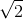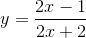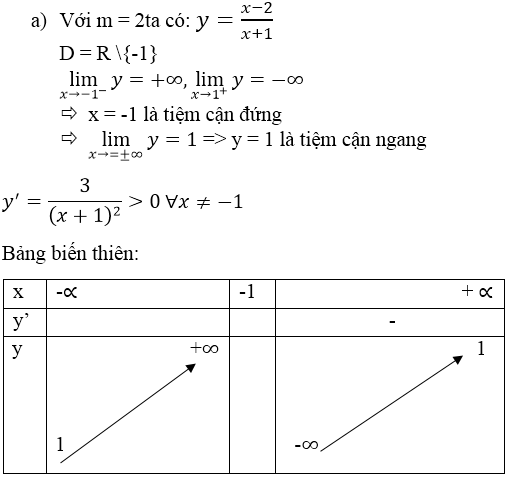
a) (0 ; -1) ∈ (G) ⇔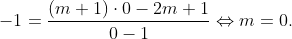
b) m = 0 ta được hàm số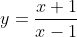
có đồ thị (G0).
(HS tự khảo sát và vẽ đồ thị).
c) (G0) cắt trục tung tại M(0 ; -1).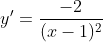
=> y'(0) = -2.
Phương trình tiếp tuyến của (G0) tại M là : y - (-1) = y'(0)(x - 0) ⇔ y= -2x - 1.