Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hướng dẫn giải:
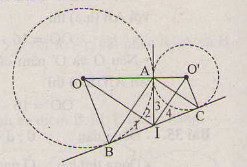
a) Theo tính chất của hai tiếp tuyến cắt nhau ta có IA=IB=IC=12BCIA=IB=IC=12BC.
Do đó tam giác ABC vuông tại A
⇒ˆBAC=90∘⇒BAC^=90∘.
b) Ta có ˆI1=ˆI2;ˆI3=ˆI4I^1=I^2;I^3=I^4 (tính chất hai tiếp tuyến cắt nhau).
Do đó ˆOIO′=90∘OIO′^=90∘ (hai tia phân giác của hai góc kề bù).
c) Ta có AI⊥OO′AI⊥OO′.
Xét tam giác OIO' vuông tại I, ta có:
IA2=OA⋅O′A=9⋅4=36⇒IA=6.IA2=OA⋅O′A=9⋅4=36⇒IA=6.
Do đó BC=12cm.
Nhận xét. Câu a), b) chỉ là gợi ý để làm câu c). Đối với những bài toán có hai đường tròn tiếp xúc, ta thường vẽ thêm tiếp tuyến chung tại tiếp điểm để xuất hiện yếu tố trung gian giúp cho việc tính toán hoặc chứng minh được thuận lợi.

a) Theo tính chất của hai tiếp tuyến cắt nhau ta có IA=IB=IC=12BCIA=IB=IC=12BC.
Do đó tam giác ABC vuông tại A
⇒ˆBAC=90∘⇒BAC^=90∘.
b) Ta có ˆI1=ˆI2;ˆI3=ˆI4I^1=I^2;I^3=I^4 (tính chất hai tiếp tuyến cắt nhau).
Do đó ˆOIO′=90∘OIO′^=90∘ (hai tia phân giác của hai góc kề bù).
c) Ta có AI⊥OO′AI⊥OO′.
Xét tam giác OIO' vuông tại I, ta có:
IA2=OA⋅O

Giả thiết:
- - Hai đường tròn (O; R) và (O'; R) cắt nhau tại A và B.
- - Vẽ các bán kính OC và O'D sao cho OC // O'D.
- - Các điểm C và D nằm cùng phía với A so với OO'.
1. Chứng minh AK // BD
- Vì OC // O'D nên ∠COB = ∠DO'B (hai góc so le trong bằng nhau).
- Mà CO và DO' là bán kính, nên tam giác COB và DO'B là hai tam giác có góc tại B bằng nhau và có cạnh OB chung.
- Xét tam giác COB và tam giác DO'B, ta có:
- ∠COB = ∠DO'B
- OB chung
→ ∠CBO = ∠DBO
- Xét tứ giác ABCD:
- A, B là giao điểm của hai đường tròn
- OC và O'D là bán kính nên CO = R = O'D
- OC // O'D ⇒ tam giác COB và DO'B đồng dạng
- Do đó: ∠CAB = ∠DBA (vì cùng bằng ∠COB)
→ ΔAKB và ΔDAB có góc tại K và D bằng nhau,
→ Mà AB là cạnh chung, nên AK // BD (góc so le trong hoặc đồng vị).
Kết luận: AK song song với BD.
2. Chứng minh A là trực tâm tam giác BCD
Ta cần chứng minh rằng A là giao điểm ba đường cao của tam giác BCD.
Ta chứng minh A nằm trên ba đường cao của tam giác BCD, tức là:
- - A là trực tâm của tam giác BCD nếu:
- -- A nằm trên đường vuông góc với CD kẻ từ B,
- -- A nằm trên đường vuông góc với BC kẻ từ D,
- -- A nằm trên đường vuông góc với BD kẻ từ C.
Cách chứng minh:
- - Vì C nằm trên đường tròn (O), D nằm trên đường tròn (O') và OC // O'D ⇒ tứ giác CODD là hình bình hành suy biến hoặc có tính chất đặc biệt.
- - Ta có OC ⊥ AB (vì tam giác COA cân tại O, góc ở A là 90 độ).
- - Tương tự, O'D ⊥ AB ⇒ AB ⊥ CD
→ Suy ra AB ⊥ CD
Tức là: A nằm trên đường vuông góc với CD kẻ từ B
- - Tương tự, ta có thể chứng minh AB ⊥ BC và AB ⊥ BD ⇒ A nằm trên hai đường cao còn lại.
Vậy A là giao điểm ba đường cao của tam giác BCD.
Kết luận: A là trực tâm tam giác BCD.🤡
Em xin tick ạ ! 🥺🥺🤡🤡🤡
Qua A, kẻ tiếp tuyến Ax với (O1) và (O2), Ax cắt BC tại K
Xét (O1) có
KB,KA là các tiếp tuyến
Do đó: KB=KA
Xét (O2) có
KA,KC là các tiếp tuyến
Do đó: KA=KC
mà KA=KB
nên KB=KC
=>K là trung điểm của BC
Xét ΔABC có
AK là đường trung tuyến
\(AK=\frac{BC}{2}\)
Do đó: ΔABC vuông tại A
=>\(\hat{BAC}=90^0\)

a: Xét (O) có
AB,AC là các tiếp tuyến
Do đó: AB=AC
=>A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1),(2) suy ra OA là đường trung trực của BC
=>OA⊥BC tại H và H là trung điểm của BC
b: Xét (O) có
ΔBCD nội tiếp
BD là đường kính
Do đó: ΔBCD vuông tại C
=>CB⊥CD
mà OA⊥BC
nên OA//CD
c: Ta có: \(\hat{FBA}+\hat{OBF}=\hat{OBA}=90^0\)
\(\hat{HBF}+\hat{OFB}=90^0\) (ΔBHF vuông tại H)
mà \(\hat{OBF}=\hat{OFB}\) (ΔOBF cân tại O)
nên \(\hat{FBA}=\hat{HBF}\)
=>BF là phân giác của góc HBA
Xét (O) có
ΔBFE nội tiếp
FE là đường kính
Do đó: ΔBFE vuông tại B
=>BF⊥BE
=>BE là phân giác ngoài tại đỉnh B của ΔHBA
Xét ΔHBA có BF là phân giác của góc HBA
nên \(\frac{FH}{FA}=\frac{BH}{BA}\left(3\right)\)
Xét ΔHBA có BE là phân giác ngoài tại đỉnh B
nên \(\frac{EH}{EA}=\frac{BH}{BA}\left(4\right)\)
Từ (3),(4) suy ra \(\frac{FH}{FA}=\frac{EH}{EA}\)
=>\(FH\cdot EA=FA\cdot EH\)
a, Chứng minh được B A C ^ = 90 0 kết hợp B A D ^ = C A E ^ = 90 0 => ĐPCM
b, Chứng minh ∆BAD:∆EAC => AD.AE=AB.AC(đpcm)
c, Chứng minh tứ giác OIO’K là hình chữ nhật
Đường tròn ngoại tiếp ∆OKO’ chính là đường tròn ngoại tiếp hình chữ nhật ,có đường kính là IK mà IK ⊥ BC tại I