Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Do A' đối xứng với A qua O nên O là trung điểm của AA' ⇒ OA = OA' = R
⇒ A' cũng thuộc đường tròn (O)

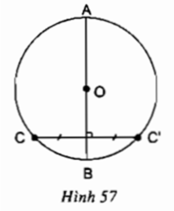
Do C và C' đối xứng nhau qua AB nên AB là đường trung trực của CC'
⇒ O nằm trên đường trung trực của CC'
⇒ OC = OC' = R
⇒ C' cũng thuộc đường tròn (O)

Do C và C' đối xứng nhau qua AB nên AB là đường trung trực của CC'
⇒ O nằm trên đường trung trực của CC'
⇒ OC = OC' = R
⇒ C' cũng thuộc đường tròn (O)

Bài 1:
a: Xét tứ giác OAMB có \(\hat{OAM}+\hat{OBM}=90^0+90^0=180^0\)
nên OAMB là tứ giác nội tiếp
=>O,A,M,B cùng thuộc một đường tròn
b: Xét ΔOAM vuông tại A và ΔOBM vuông tại B có
OM chung
OA=OB
Do đó: ΔOAM=ΔOBM
=>MA=MB
c: OA=OB
=>O nằm trên đường trung trực của AB(1)
ta có: MA=MB
=>M nằm trên đường trung trực của AB(2)
Từ (1),(2) suy ra OM là đường trung trực của AB
d: OM là đường trung trực của AB
=>OM⊥AB tại H và H là trung điểm của AB
Xét ΔOAM vuông tại A có AH là đường cao
nên \(OH\cdot OM=OA^2=R^2\) không đổi
Bài 2:
a; Xét (O) có
ΔAEB nội tiếp
AB là đường kính
Do đó:ΔAEB vuông tại E
=>BE⊥MA tại E
Xét (O) có
ΔAFB nội tiếp
AB là đường kính
Do đó: ΔAFB vuông tại F
=>AF⊥MB tại F
b: Xét tứ giác MEHF có \(\hat{MEH}+\hat{MFH}=90^0+90^0=180^0\)
nên MEHF là tứ giác nội tiếp đường tròn đường kính MH
=>M,E,H,F cùng thuộc một đường tròn
c: Vì MEHF nội tiếp đường tròn đường kính MH
mà I là trung điểm của MH
nên IM=IE=IF=IH
Gọi K là giao điểm của MH và AB
Xét ΔMAB có
AF,BE là các đường cao
AF cắt BE tại H
Do đó: H là trực tâm của ΔAMB
=>MH⊥AB tại K
IE=IH
=>ΔIEH cân tại I
=>\(\hat{IEH}=\hat{IHE}\)
=>\(\hat{IEH}=\hat{KHB}\)
\(\hat{IEO}=\hat{IEH}+\hat{OEH}\)
\(=\hat{KHB}+\hat{OBH}=\hat{KHB}+\hat{KBH}=90^0\)
=>IE⊥OE
d: Xét ΔIEO và ΔIFO có
IE=IF
OE=OF
IO chung
Do đó: ΔIEO=ΔIFO
=>\(\hat{IEO}=\hat{IFO}=90^0\)
=>I,E,O,F cùng thuộc một đường tròn

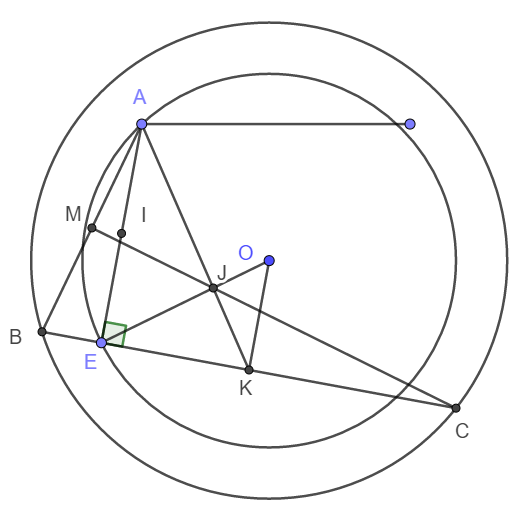
a) Gọi I, K lần lượt là trung điểm của AE và BC.
Ta có : \(EB^2=\left(BK-EK\right)^2;EC^2=\left(KC+EK\right)^2\)
\(\Rightarrow EB^2+EC^2=2\left(BK^2+EK^2\right)=2\left(BO^2-OK^2+OE^2-OK^2\right)\)
\(=2\left(R^2+r^2\right)-4OK^2\)
\(AE^2=4AI^2=4\left(r^2-OI^2\right)\)
\(\Rightarrow EB^2+EC^2+EA^2=2R^2+6r^2-4\left(OI^2+OK^2\right)\)
Mà OIEK là hình chữ nhật nên \(OI^2+OK^2=OE^2=r^2\)
\(\Rightarrow EB^2+EC^2+EA^2=2R^2+2r^2\) không đổi.
b) Giả sử EO giao với AK tại J.
Vì IOEK là hình chữ nhật nên OK song song và bằng EI. Vậy nên OK song song và bằng một nửa AE.
Do đó \(\frac{JE}{JO}=\frac{AJ}{JK}=\frac{AE}{OK}=2\)
Vì OE cố định nên J cố định; Vì AK là trung tuyến của tam giác ABC nên J là trọng tâm tam giác ABC
Suy ra J thuộc MC.
Vậy MC đi qua J cố định.
c) Vì AK = 3/2AJ nên H trùng K.
Do đó OH vuông góc BC. Suy ra H thuộc đường tròn đường kính OE.
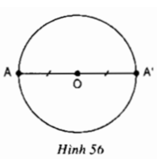
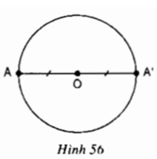
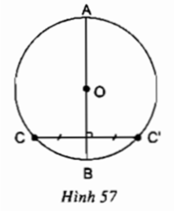


Do A' đối xứng với A qua O nên O là trung điểm của AA' ⇒ OA = OA' = R
⇒ A' cũng thuộc đường tròn (O)