Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Nhiệt lượng
\(Q=I^2Rt=\frac{E^2_0t}{2R}=\frac{\left(\omega NBS\right)^2t}{2R}=\frac{\left(200.100\pi.0,002\right)^2.60}{2.1000}\)\(=474J\)

Phương pháp: Áp dụng công thức tính nhiệt lượng Q = I 2 Rt
Đáp án C
Từ phương trình dòng điện, ta có I0 = 5A Nhiệt lượng tỏa ra trên điện trở
Cách giải: Đáp án C
+ Từ phương trình dòng điện, ta có I0 = 5A Nhiệt lượng tỏa ra trên điện trở
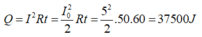

Nhiệt lượng tỏa ra: \(Q=P.t=I^2R.t\)
\(\Rightarrow I=\sqrt{\frac{Q}{Rt}}=\sqrt{\frac{6000}{25.2.60}}=\sqrt{2}A\)

Nhiệt lượng tỏa ra trên điện trở
\(Q=I^2Rt=2^2.100.30=12000J=12kJ\)

\(L = \frac{1}{\omega^2 C}=0,625H.\)
\(i = 0,02. \cos8000.\frac{\pi}{48000}= 0,02.\cos\frac{\pi}{6}= 0,02.\frac{\sqrt{3}}{2}\)
\(W_C=\frac{1}{2}L(I_0^2-i^2) = 3,125.10^{-5}J.\)

\(W= W_{Cmax}=W_C+W_L\)
=> \(W_L = W_{Cmax}-W_C= \frac{1}{2}C.(U_0^2-u^2)= 5.10^{-7}J.\)

Nhiệt lượng do dòng điện tỏa ra trên điện trở:
\(Q=I^2Rt=\left(\sqrt{2}\right)^2.10.30=600J\)

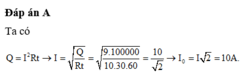
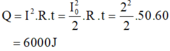
Đáp án C
+ Từ phương trình dòng điện, ta có I 0 = 5 A
Nhiệt lượng tỏa ra trên điện trở