Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lục giác DPEQFM có các cặp cạnh đối bằng nhau từng đôi một:
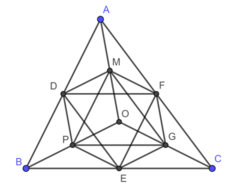
DP = QF (vì bằng 1/2 OA);
PE = MF (vì bằng 1/2 OC)
EQ = MD (vì bằng 1/2 OB)
Lục giác DPEQFM có 6 cạnh bằng nhau chỉ khi DP = PE = EQ.
Muốn vậy, ta phải có OA = OB = OC, khi đó O là điểm cách đều ba điểm A, B, C. Vậy O là giao điểm của ba đường trung trực tam giác ABC.

a) Vì O lầ điểm cách đều 3 cạnh của \(\Delta ABC\) nên:
+) \(OD=OE=OF\)
+) \(AO\), \(BO\) và \(CO\) là 3 đường phân giác của \(\Delta ABC\)
Xét \(\Delta BFO\) và \(\Delta BDO\) có:
\(\widehat{BFO}\)=\(\widehat{BDO}\)=90o
\(BO\) chung
\(OF=OD\) (CMT)
\(\Rightarrow\Delta BFO=\Delta BDO\) (ch-cgv)
\(\Rightarrow BF=BD\)
\(\Rightarrow\Delta BFD\) cân tại \(B\)
\(\Rightarrow\widehat{BFD}\)=\(\widehat{BDF}\)= ( \(180^o\)- \(\widehat{FBD}\)) : 2 \(\left(1\right)\)
Vì \(BA=BM\) (gt) nên \(\Delta BAM\) cân tại \(B\)
\(\Rightarrow\widehat{BAM}\)=\(\widehat{BMA}\)= (\(180^o\)-\(\widehat{ABM}\)) : 2 \(\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\) \(\Rightarrow\widehat{BFD}\)=\(\widehat{BAM}\) mà chúng ở vị trí đồng vị nên \(DF\)//\(AM\)
\(\Rightarrow\) Tứ giác \(AFDM\) là hình thang \(\left(3\right)\)
Từ \(\left(2\right)\) và \(\left(3\right)\) \(\Rightarrow\) \(AFDM\) là hình thang cân
\(\Rightarrow\) \(MF=AD\) \(\left(4\right)\)
CM tương tự ta được: \(AEDN\) là hình thang cân
\(\Rightarrow\) \(NE=AD\) \(\left(5\right)\)
Từ \(\left(4\right)\) và \(\left(5\right)\) \(\Rightarrow MF=NE\)
b) Xét \(\Delta ODM\) và \(\Delta OFA\) có:
\(OD=OF\) (CMT)
\(\widehat{ODM}\)=\(\widehat{OFA}\)=\(90^o\)
\(OM=FA\) (\(AFDM\) là hình thang cân)
\(\Rightarrow\Delta ODM=\Delta OFA\) (c.g.c)
\(\Rightarrow OM=OA\left(6\right)\)
CM tương tự ta được \(\Delta ODN=\Delta OEA\) (c.g.c)
\(\Rightarrow\)\(ON=OA\) \(\left(7\right)\)
Từ \(\left(6\right)\) và \(\left(7\right)\) \(\Rightarrow OM=ON\)
\(\Rightarrow\) \(\Delta MON\) cân tại \(O\)
Mình biết bài này là từ 2019 rồi nhưng mà đề này mình thấy chưa ai làm nên mình làm để có bạn nào tìm thì sẽ có để tham khảo.
vâng baayh là 2022 r nhưng e vẫn tìm câu trl của tiền bối ạ :33
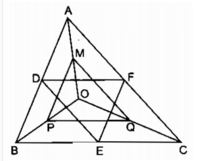
Vì ∆ABC đều
=> A = B = C
Vì OD // BC ( gt)
=> ODEB là hình thang
Vì OE//AC(gt)
=> C = DEB ( đồng vị)
Mà B = C
=> B = DEB
=> DOEB là hình thang cân
Vì OE // AC
=> EOFC là hình thang
Vì OF//AB
=> A = BFC ( đồng vị)
Mà A = C (cmt)
=> C = BFC
=> EOFC là hình thang cân
Vì OF // AB
=> FODA là hình thang
Mà OD //BC
=> ADF = B
Mà A = B
=> A = ADF
=> FODA là hình thang cân
Vì DOEB là hình thang cân
Mà B = OEB = 60°
=> BDO = DOE = 120°
Chứng minh tương tự ta có
DOE = DOF = FOD = 120°
Trong hình thang cân hai đường chéo bằng nhai
=> OA = DF
=> OB = DE
=> OC = EF
Vì 3 đoạn thẳng OA ; OB ; OC lần lượt là bằng 3 cạnh của ∆DEF
=> 3 đoạn thẳng OA ; OB ; OC thỏa mãn bất đẳng thức tam giác