K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

17 tháng 5 2023
góc ONM=góc ONH+góc MNB
=góc OHN+góc MNB
=góc NBC+góc MHB=90độ
=>MN là tiếp tuyến của (O)

CM
16 tháng 9 2017
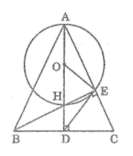
Ta có : OH = OE
Suy ra tam giác OHE cân tại O
![]()
Trong tam giác BDH ta có:
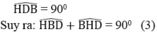
Từ (1), (2) và (3) suy ra:
![]()
Tam giác ABC cân tại A có AD ⊥ BC nên BD = CD
Tam giác BCE vuông tại E có ED là đường trung tuyến nên:
ED = DB = BC/2 (tính chất tam giác vuông)
Suy ra tam giác BDE cân tại D
![]()
Suy ra: DE ⊥ EO. Vậy DE là tiếp tuyến của đường tròn (O).

Gọi O là trung điểm AH, tam giác AHN vuông tại N nên N thuộc đường tròn đường kính AH
Do ABC cân tại A \(\Rightarrow\) AM là đường cao đồng thời là trung tuyến
\(\Rightarrow\) M là trung điểm BC
Trong tam giác vuông NBC, NM là trung tuyến ứng với cạnh huyền
\(\Rightarrow MN=MB=\dfrac{1}{2}BC\Rightarrow\Delta MNB\) cân tại M
\(\Rightarrow\widehat{MNB}=\widehat{MBN}\) (1)
Tương tự, trong tam giác vuông ANH, ta có: \(ON=OH=\dfrac{1}{2}AH\Rightarrow\widehat{ONH}=\widehat{OHN}\)
Mà \(\widehat{OHN}=\widehat{MHB}\) (đối đỉnh) \(\Rightarrow\widehat{ONH}=\widehat{MHB}\) (2)
Lại có tam giác HBM vuông tại M \(\Rightarrow\widehat{MHB}+\widehat{MBN}=90^0\) (3)
(1);(2);(3) \(\Rightarrow\widehat{ONH}+\widehat{MNB}=90^0\) hay \(MN\perp ON\)
\(\Rightarrow MN\) là tiếp tuyến của đường tròn đường kính AH