K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

24 tháng 8
a) Chứng minh \(\triangle A D M = \triangle N I C\)
- Ta có: \(D M \parallel B C\), mà \(N I \parallel A B\).
⇒ \(\triangle A D M\) và \(\triangle N I C\) có: - \(\hat{A D M} = \hat{N I C}\) (so le trong).
- \(\hat{D A M} = \hat{N C I}\) (so le trong).
- Ngoài ra: \(A D = B E\). Do \(B E\) đối xứng với \(A D\) trên cùng cạnh \(A B\), mà \(N I \parallel A B\) ⇒ \(A D = N I\).
⇒ \(\triangle A D M = \triangle N I C\) (theo trường hợp c.g.c).
b) Chứng minh \(D M + E N = B C\)
- Do \(D M \parallel B C\), tứ giác \(A D M C\) là hình thang.
- Tương tự, do \(E N \parallel B C\), tứ giác \(B E N C\) là hình thang.
- Trong \(\triangle A D M = \triangle N I C\) (chứng minh trên), ta có:
\(D M = I C\)
- Lại có \(E N \parallel B C\) ⇒ \(E N = B I\).
⇒ Cộng lại:
\(D M + E N = I C + B I = B C .\)

6 tháng 12 2016
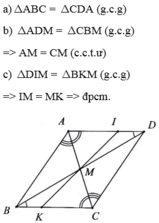
qua N kẻ đường thẳng song song với AB cắt BC tại K .
Vì EN song song với BK; NK song song với EB nên EB=NK;EN=BK (tính chất đoạn chắn)
nên NK=AD. Vì DM song song với BC nên góc( từ sau góc mình kí hiệu là >) DMA = >ACB . Vì NK song song với AB nên >A= >KNC \(\Rightarrow\) >B=>NKC Do đó ΔADM=ΔNKC (g.c.g). nên DM=KC
Suy ra DM+EN=BK+CK=BC(dpcm)