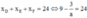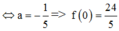![]()
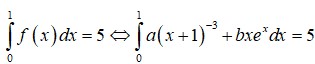
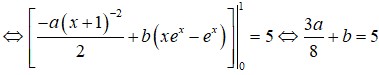
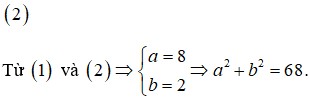
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

![]()
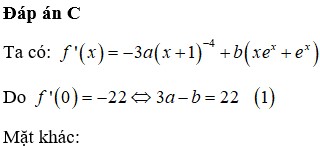
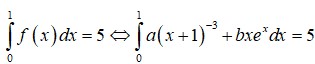
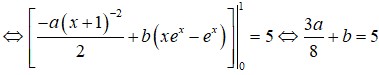
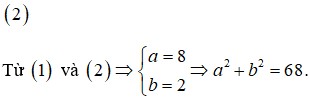

Đáp án A
Ta có:
∫ 0 1 f x d x = ∫ 0 1 a x + 1 3 d x + ∫ 0 1 b x e x d x = − a 2 1 x + 1 2 0 1 + ∫ 0 1 b x e x d x = 3 a 8 + ∫ 0 1 b x e x d x
Đặt:
u = x d v = e x d x ⇒ d u = d x v = e x ⇒ ∫ 0 1 b x e x d x = b x e x 0 1 − ∫ 0 1 b e x d x = b x e x 0 1 − b e x 0 1 = b
Suy ra ∫ 0 1 f x d x = 3 a 8 + b = 5 1
Mặt khác f ' x = − 3 a x + 1 4 + b e x + b x e x ⇒ f ' 0 = − 3 a + b = − 22 2
Từ 1 , 2 suy ra a = 8 ; b = 2 ⇒ a + b = 10

Ta có:
\(f\left(1\right).f\left(-1\right)=\left(a+b\right).\left(-a+b\right)\)
\(\Rightarrow\left(a+b\right)\left(-a+b\right)=\left(a+b\right)^2\)
\(\Rightarrow-a+b=a+b\)
\(\Rightarrow a=-a\)
\(a\ne0\) thì làm sao có a thỏa mãn được?
Trần Thùy Dung ko biết thì đừng có làm. 5 - 3a - 3b = 5. Bài này trong violympic.

a/ f(x) = 0 => x2 + 4x - 5 = 0 => (x - 1)(x + 5) = 0 => x = 1 hoặc x = -5
Vậy x = 1 , x = -5
b/ f(x) > 0 => x2 + 4x - 5 > 0 => (x - 1)(x + 5) > 0 => x - 1 > 0 và x + 5 > 0 => x > 1 và x > -5 => x > 1
hoặc x - 1 < 0 và x + 5 < 0 => x < 1 và x < -5 => x < -5
Vậy x > 1 hoặc x < -5
c/ f(x) < 0 => x2 + 4x - 5 < 0 => (x - 1)(x + 5) < 0 => x - 1 > 0 và x + 5 < 0 => x > 1 và x < -5 => vô lí
hoặc x - 1 < 0 và x + 5 > 0 => x < 1 và x > -5 => -5 < x < 1
Vậy -5 < x < 1

Có:
\(f\left(x_1\right)=ax_1+b=0\)
\(f\left(x_2\right)=ax_2+b=0\)
\(\Rightarrow f\left(x_1\right)-f\left(x_2\right)=0-0\)
\(\Rightarrow a\left(x_1-x_2\right)=0\)
\(x_1\ne x_2\Rightarrow x_1-x_2\ne0\)
\(\Rightarrow a=0\)
\(\Rightarrow f\left(x_1\right)=0=0+b\Rightarrow b=0\)
Như vậy với mọi giá trị của x thì đa thức trên luôn bằng 0.
Vậy f(x) là đa thức 0.

Đáp án D
Ta có ∫ 0 1 f x d x = ∫ 0 1 a x + 1 3 d x + ∫ 0 1 b x e x d x = − a 2 1 x + 1 2 0 1 + ∫ 0 1 b x e x d x = 3 a 8 + ∫ 0 1 b x e x d x .
Đặt u = x d v = e x ⇒ d u = d x v = e x ⇒ ∫ 0 1 b x e x d x = b x e x − 0 1 ∫ 0 1 b e x d x = b x e x 0 1 − b e x 0 1 = b .
Suy ra ∫ 0 1 f x d x = 3 a 8 + b = 5 1 .
Mặt khác f ' x = − 3 a x + 1 4 + b e x + b x e x ⇒ f ' 0 = − 3 a + b = − 22 2
Từ (1) và (2) suy ra a = 8 ; b = 2 ⇒ a + b = 10.

Đáp án C
Giả sử ![]()
Hoành độ điểm D là nghiệm phương trình: ![]()
![]()
![]()
![]()
Hoành độ điểm E là nghiệm của phương trình: ![]()
![]()
![]()
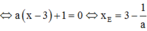
Hoành độ điểm F là nghiệm của phương trình: ![]()
![]()
![]()
![]()
Khi đó