Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 1 : D
Câu 2 : D
Câu 3 : C
Câu 4 : Tam giác luôn là "tam giác đơn", "tam giác lồi" vì số đo các góc trong luôn nhỏ hơn 1800.
Câu 5 : Sai. Vì không có tam giác nào có trọng tâm nằm ngoài tam giác.

a) Ta có 3 – 2 < 6 < 3 + 2
2cm, 3cm, 6cm không là ba cạnh của tam giác.
b) Vì 6 = 2 + 4
2cm, 4cm, 6cm không là 3 cạnh của một tam giác
c) 4 – 3 < 6 < 4 + 3
3cm, 4cm, 6cm là 3 cạnh của một tam giác.
TK NHA !!!
a) Ta có 3 – 2 < 6 < 3 + 2 bất đẳng thức này sai nên ba độ dài 2cm, 3cm, 6cm không là ba cạnh của tam giác.
b) Vì 6 = 2 + 4 nên ba độ dài là 2cm, 4cm, 6cm không là 3 cạnh của một tam giác
c) 4 – 3 < 6 < 4 + 3 bất đẳng thức đúng nên ba độ dài 3cm, 4cm, 6cm là 3 cạnh của một tam giác.
K NHÉ!!!!!!!

a) Vì 2 + 3 < 6 (trái với bất đẳng thức tam giác) nên 3 độ dài này không thể là 3 cạnh của 1 tam giác.
b) Vì 2 + 4 = 6 (trái với bất đẳng thức tam giác) nên 3 độ dài này không thể là 3 cạnh của 1 tam giác.
c) Vì 3 + 4 > 7 (thỏa mãn bất đẳng thức tam giác) nên 3 độ dài này là 3 cạnh của 1 tam giác
Vẽ hình tam giác có 3 cạnh 3, 4, 7 dùng compa và thước thẳng để vẽ (Tham khảo trong sách giáo khoa)
Chúc học tốt!

Bài toán này yêu cầu tìm điểm \(M\) trên cạnh \(B C\) của tam giác \(A B C\) sao cho nếu vẽ các điểm \(D\) và \(E\) sao cho \(A B\) là đường trung trực của \(M D\) và \(A C\) là đường trung trực của \(M E\), thì độ dài đoạn \(D E\) là nhỏ nhất.
Phân tích bài toán:
Để giải bài toán này, ta cần tìm điểm \(M\) sao cho đoạn thẳng \(D E\) có độ dài nhỏ nhất. Để làm được điều này, ta cần hiểu rằng khi \(M\) được chọn sao cho \(A B\) và \(A C\) là các đường trung trực của \(M D\) và \(M E\), thì \(D\) và \(E\) là các điểm đối xứng của \(M\) qua các đường trung trực tương ứng.
Điều này gợi ý về tính chất đối xứng trong tam giác và liên quan đến điểm đối xứng của tam giác.
Hướng giải:
- Xác định các đối xứng:
- \(A B\) là đường trung trực của \(M D\), nghĩa là \(D\) là ảnh của \(M\) qua đường thẳng \(A B\).
- \(A C\) là đường trung trực của \(M E\), nghĩa là \(E\) là ảnh của \(M\) qua đường thẳng \(A C\).
- Điều kiện để đoạn \(D E\) có độ dài nhỏ nhất:
Để \(D E\) có độ dài nhỏ nhất, điểm \(M\) cần phải được chọn sao cho điểm \(D\) và \(E\) có thể đối xứng nhau một cách tối ưu nhất qua các đường trung trực. Từ đó, ta có thể suy ra rằng điểm \(M\) phải là điểm đối xứng của điểm \(A\) qua cạnh \(B C\), tức là \(M\) phải là vị trí đối xứng của \(A\) qua đường thẳng \(B C\). - Lý do:
Khi \(M\) là điểm đối xứng của \(A\) qua \(B C\), thì các đường trung trực của \(M D\) và \(M E\) (tức là các đường vuông góc với \(A B\) và \(A C\)) sẽ tạo thành một hệ đối xứng đặc biệt, dẫn đến việc đoạn \(D E\) có độ dài nhỏ nhất.
Kết luận:
Điểm \(M\) trên cạnh \(B C\) sao cho đoạn \(D E\) có độ dài nhỏ nhất chính là điểm đối xứng của điểm \(A\) qua đường thẳng \(B C\).

a) Với 3 độ dài 2cm, 3cm, 4cm lập thành 3 cạnh của tam giác.
b) 1cm; 2cm; 3,5cm không lập thành 3 cạnh của tam giác vì 2 – 1 < 3,5 < 2 + 1 bất đẳng thức sai
c) 2,2 + 2 = 4,2 không lập thành tam giác
a) 1cm + 2cm = 3cm < 4cm
⇒ bộ ba đoạn thẳng 1cm, 2cm, 4cm không thể tạo thành 1 tam giác.
b) 2cm + 3cm = 5cm.
⇒ Bộ ba đoạn thẳng 2cm; 3cm; 5cm không lập thành tam giác.
c) Ta có 3cm + 4cm = 7cm > 5cm.
Do đó bộ đoạn thẳng 3cm, 4cm, 5cm có thể thành 3 cạnh của tam giác.
Cách dựng tam giác có ba độ dài 3cm, 4cm, 5cm :
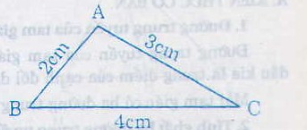
- Vẽ BC = 4cm
- Dựng đường tròn tâm B bán kính 2cm ; đường tròn tâm C bán kính 3cm. Hai đường tròn cắt nhau tại A. Nối AB, AC ta được tam giác cần dựng.