Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Bài 7:
a; 3\(^{x}\).3 = 243
3\(^{x+1}\) = 3\(^5\)
\(x+1\) = 5
\(x=5-1\)
\(x=4\)
Vậy \(x=4\)
b; 2\(^{x}\).162 = 1024
\(2^{x}\) = 1024 : 162
2\(^{x}\) = \(\frac{512}{81}\) (loại vì 512/81 không phải là số tự nhiên)
Không có số tự nhiên nào của x thỏa mãn đề bài.
Vậy \(x\in\) ∅
c; 64.4\(^{x}\) = 168
4\(^{x}\) = 168 : 64
4\(^{x}\) = \(\frac{21}{8}\) (loại)
vì 21/8 không phải là số tự nhiên
Vậy \(x\in\) ∅
d; \(2^{x}\) = 16
\(2^{x}\) = 2\(^4\)
\(x=4\)
Vậy \(x=4\)
Bài 8:
a; (\(2^{17}\) + 17\(^2\)).(9\(^{15}\) - 3\(^{15}\)).(2\(^4\) - 4\(^2\))
= (\(2^{17}\) + 17\(^2\)).(9\(^{15}\) - 3\(^{15}\)).(16 - 16)
= (\(2^{17}\) + 17\(^2\)).(9\(^{15}\) - 3\(^{15}\)).0
= 0
b; (\(8^{2017}\) - 8\(^{2015}\)):(8\(^{2014}\).8\(\))
= (\(8^{2017}\) - 8\(^{2015}\)): \(8^{2015}\)
= \(8^{2017}:8^{2015}\) - \(8^{2015}\) : 8\(^{2015}\)
= 8\(^2\) - 1
= 64 - 1
= 63
c; (1\(^3\) + 2\(^3\) + 3\(^4\) + 4\(^5\)).(\(3^8-81^2\))
= (1\(^3\) + 2\(^3\) + 3\(^4\) + 4\(^5\)).(3\(^8\) - 3\(^8\))
= (1\(^3\) + 2\(^3\) + 3\(^4\) + 4\(^5\)).0
= 0
d; (2\(^8\) + 8\(^3\)) : (2\(^5\).2\(^3\))
= (2\(^8\) + 2\(^9\)):(2\(^8\))
= 2\(^8\) : 2\(^8\) + 2\(^9\) : 2\(^8\)
= 1 + 2
= 3
Olm chào em, em cần làm gì với biểu thức này thi ghĩ rõ yêu cầu ra, em nhé.
\( [(8𝑥 - 12) ∶ 4]. 33 = 36\)
\([(8𝑥-12)∶4]=36:33\)
\([(8𝑥-12)∶4]=\frac{36}{33}\)
\([(8𝑥-12)∶4]=\frac{12}{11}\)
\((8𝑥-12)=\frac{12}{11}.4\)
\((8𝑥-12)=\frac{48}{11}\)
\(8x=\frac{48}{11}+12\)
\(8x=\frac{48}{11}+\frac{132}{11}\)
\(8x=\frac{180}{11}\)
\(x=\frac{180}{11}\text{:8}\)
\(x=\frac{180}{11}\frac{.1}{8}\)
\(x=\frac{180}{88}\)
\(x=\frac{45}{22}\)
Vậy \(x=\frac{45}{22}\)
[(8x−12)∶4].33=36
\(\left[\right. \left(\right. 8 x - 12 \left.\right) ∶ 4 \left]\right. = 36 : 33\)
\(\left[\right. \left(\right. 8 x - 12 \left.\right) ∶ 4 \left]\right. = \frac{36}{33}\)
\(\left[\right. \left(\right. 8 x - 12 \left.\right) ∶ 4 \left]\right. = \frac{12}{11}\)
\(\left(\right. 8 x - 12 \left.\right) = \frac{12}{11} . 4\)
\(\left(\right. 8 x - 12 \left.\right) = \frac{48}{11}\)
\(8 x = \frac{48}{11} + 12\)
\(8 x = \frac{48}{11} + \frac{132}{11}\)
\(8 x = \frac{180}{11}\)
\(x = \frac{180}{11} :\text{8}\)
\(x = \frac{180}{11} \frac{. 1}{8}\)
\(x = \frac{180}{88}\)
\(x = \frac{45}{22}\)
Vậy \(x = \frac{45}{22}\)
(x+2)(16-x)=15
=>(x+2;16-x)∈{(1;15);(15;1);(-1;-15);(-15;-1);(3;5);(5;3);(-5;-3);(-3;-5)}
x+2 | 1 | 15 | -1 | -15 | 3 | 5 | -5 | -3 |
x | -1 | 13 | -3 | -17 | 1 | 3 | -7 | -5 |
16-x | 15 | 1 | -15 | -1 | 5 | 3 | -3 | -5 |
x | 1 | 15 | 31 | 17 | 11 | 13 | 19 | 21 |
Theo Bảng, ta có: không có giá trị nguyên nào của x thỏa mãn yêu cầu bài toán, hay bài toán chỉ có giá trị thực
(x+2)(16-x)=15
=>\(16x-x^2+_{}32-2x=15\)
=>\(-x^2+14x+17=0\)
=>\(x^2-14x-17=0\)
=>\(x^2-14x+49-66=0\)
=>\(\left(x-7\right)^2=66\)
=>\(\left[\begin{array}{l}x-7=\sqrt{66}\\ x-7=-\sqrt{66}\end{array}\right.\Rightarrow\left[\begin{array}{l}x=\sqrt{66}+7\\ x=-\sqrt{66}+7\end{array}\right.\)
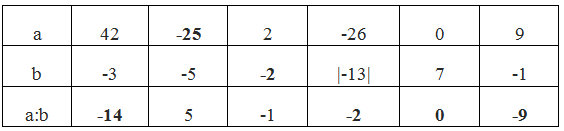
| A | 42 | -25 | 2 | -26 | 0 | 9 |
| B | -3 | -5 | -1 | 13 | 7 | -1 |
| A : B | -14 | 5 | -2 | -2 | 0 | -9 |
| m | 4 | -13 | -5 | |
| n | -6 | 20 | -20 | |
| m.n | -260 | -100 |
Là như thế này :
m = 4
n = -6
m.n = ?
bạn sẽ lấy 4 . ( -6 ) sẽ bằng 24 ( bạn phải đọc kĩ ghi nhớ trong sách giáo khoa ) nhưng bạn phải nhớ nhân số nguyên khác dấu với số nào đó ta sẽ nhân giống như bình thường và đặt dấu " - " trước số đó , như vậy sẽ tìm ra kết quả
Còn : m = ?
n = -20
m.n = -260
Thì bạn lấy -260 chia cho -20 thì sẽ ra kết quả thôi
mk hiểu đến đâu mk giảng đến đó nha , không hiểu chỗ nào bảo mk giảng lại
Chúc bạn học tốt !
Sách Giáo Khoa
Bài giải:
|
a |
-15 |
13 |
-4 |
9 |
-1 |
|
b |
6 |
-3 |
-7 |
-4 |
-8 |
|
ab |
-90 |
-39 |
28 |
-36 |
8 |
- Tích số là dương:
+ Nếu một thừa số là dương thì thừa số còn lại cũng là dương.
+ Nếu một thừa số là âm thì thừa số còn lại phải là âm.
- Tích số là âm:
+ Nếu một thừa số là dương thì thừa số còn lại phải là âm.
+ Nếu một thừa số là âm thì thừa số còn lại phải là dương.
a) Ta có bảng sau:
a
9
34
120
15
2 987
b
12
51
70
28
1
ƯCLN(a, b)
3
17
10
1
1
BCNN(a, b)
36
102
840
420
2 987
ƯCLN(a, b) .BCNN(a, b)
108
1 734
8 400
420
2 987
a.b
108
1 734
8 400
420
2 987
Giải thích:
+) Ở cột thứ hai:
a = 34 = 2.17; b = 51 = 3.17
⇒ ƯCLN(a; b) = 17 ; BCNN(a; b) = 2.3.17 = 102.
ƯCLN(a, b) . BCNN(a, b) = 17.102 = 1 734.
a.b = 34. 51 = 1 734.
+) Ở cột thứ ba:
a = 120 =\(2^3.3.5\) ; b = 70 = 2.5.7
⇒ ƯCLN(a, b) = 2. 5 = 10 ; BCNN(a, b) =\(2^3.3.5.7\)= 840
ƯCLN(a, b) . BCNN(a, b) = 10. 840 = 8 400.
a.b = 120. 70 = 8 400.
+) Ở cột thứ tư:
a = 15 =3.5; b =\(28 = 2^2.7\)
⇒ ƯCLN(a, b) = 1 ; BCNN(a, b) = \(2^2.3.5.7\)=420
ƯCLN(a, b) . BCNN(a, b) =1. 420 = 420.
a.b = 15. 28 = 420.
+) Ở cột thứ năm:
a = 2 987; b = 1
⇒ ƯCLN(a; b) = 1 ; BCNN(a; b) = 2 987
ƯCLN(a, b) . BCNN(a, b) = 1 . 2 987 = 2 987.
a.b = 2 987 . 1 = 2 987
b) ƯCLN(a, b).BCNN(a, b) = a.b
Em rút ra kết luận: tích của BCNN và ƯCLN của hai số tự nhiên bất kì bằng tích của chúng.