Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Tứ giác AEDF là hình bình hành.
Vì có DE // AF, DF // AE (gt) (theo định nghĩa)
b) Hình bình hành AEDF là hình thoi khi AD là tia phân giác của góc A. Vậy nếu D là giao điểm của tia phân giác góc A với cạnh BC thì AEDF là hình thoi.
.

c) Giả thuyết: tứ giác ANMP là hình chữ nhật thì hình bình hành ANMP vuông tại A
=> \(\Delta ABC\)vuông tại A
Vậy: DK để tứ giác ANMP là hình chữ nhật thì \(\Delta ABC\)phải vuông tại A
d) Để tứ giác ANMP là hình vuông thì:
+ Tứ giác ANMP phải là hình thoi
+ Tứ giác ANMP có 1 góc vuông
(Dựa vào DHNB thứ 4: Hình thoi có một góc vuông là hình vuông)
Do đó: Để tứ giác ANMP là hình vuông thì: M phải là giao điểm của phân giác góc A và cạnh BC; đồng thời tứ giác ANMP có một góc vuông tại A(kết hợp kết quả câu b và c)
Hok tốt ~

Hình bạn tự vẽ nhé!
c) Bạn có: EFGD là hình bình hành
=> FG // ED
FG = ED
Mà FG = FA ; ED = EK
=> AG // DK
AG = DK
=> AGDK là hình bình hành
Lại có O là trung điểm AD
=> O là trung điểm GK
=> G đối xứng K qua O
d) Mình làm tắt:
Để AIGD là hình vuông thì
\(\hept{\begin{cases}AD\perp GD\\AD=GD\end{cases}}\)
\(\Rightarrow\Delta ABC\)vuông cân

a) Tứ giác AEDF là hình bình hành.
Vì có DE // AF, DF // AE (gt) (theo định nghĩa)
b) Hình bình hành AEDF là hình thoi khi AD là tia phân giác của góc A. Vậy nếu D là giao điểm của tia phân giác góc A với cạnh BC thì AEDF là hình thoi.
c) Nếu ΔABC vuông tại A thì AEDF là hình chữ nhật (vì là hình bình hành có một góc vuông).
d) Nếu ABC vuông tại A và D là giao điểm của tia phân giác của góc A với cạnh BC thì AEDF là hình vuông (vì vừa là hình chữ nhật, vừa là hình thoi).
A E F C D B
a) Tứ giác AEDF là hình bình hành.
Vì có DE // AF, DF // AE (gt)
(theo định nghĩa)
b) Hình bình hành AEDF là hình thoi khi AD là tia phân giác của góc A với cạnh BC thì AEDF là hình thoi.
c) Nếu ∆ABC vuông tại A thì AEDF là hình chữ nhật (vì là hình bình hành có một góc vuông).
Nếu ABC vuông tại A và D là giao điểm của tia phân giác của góc A với cạnh BC thì AEDF là hình vuông (vì vừa là hình chữ nhật vừa là hình thoi).

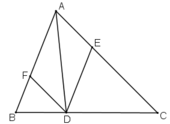
a) Tứ giác AEDF là hình bình hành.
Vì có DE // AF, DF // AE (gt) (theo định nghĩa)
b) Hình bình hành AEDF là hình thoi khi AD là tia phân giác của góc A. Vậy nếu D là giao điểm của tia phân giác góc A với cạnh BC thì AEDF là hình thoi.
c) Nếu ΔABC vuông tại A thì AEDF là hình chữ nhật (vì là hình bình hành có một góc vuông).
d) Nếu ABC vuông tại A và D là giao điểm của tia phân giác của góc A với cạnh BC thì AEDF là hình vuông (vì vừa là hình chữ nhật, vừa là hình thoi).