K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
🤔
HH
10 tháng 8 2017
Ta có: \(\dfrac{1}{299}+\dfrac{4}{299}+\dfrac{7}{299}+...+\dfrac{298}{299}\) \(=\dfrac{1+4+7+...+298}{299}\)
Tính riêng mãu ta được: \(1+4+7+...+298=\dfrac{\left[\left(298-1\right):3+1\right].\left(298+1\right)}{2}\)
\(=14950\)
Ghép vào vs mẫu ta được: \(\dfrac{14950}{299}\) \(=50\)
Vậy \(\dfrac{1}{299}+\dfrac{4}{299}+\dfrac{7}{299}+...+\dfrac{298}{299}=50\).
MV
10 tháng 8 2017
rối mắt quá nhá
\(\dfrac{1}{299}+\dfrac{4}{299}+\dfrac{7}{299}+...+\dfrac{298}{299}\\ =\dfrac{1+4+7+...+298}{299}\\ =\dfrac{\left(\dfrac{298-1}{3}+1\right)\cdot\left(298+1\right)}{2}:299\\ =\dfrac{100\cdot299}{2}\cdot\dfrac{1}{299}\\ =\dfrac{100\cdot299}{2\cdot299}\\ =50\)
🌸
💸
❤
⛽
🍚
🍙
💰
👮🏻
🎉
🌺Cung chúc tân niên,
🌹Sức khoẻ vô biên,
💪
♐
🌞Hạnh phúc triền miên 
💖
🍀Túi luôn đầy tiền 
💵
💐Sung sướng như tiên,
😇
✨
😘
🌟° 
🔷
💫
🔴
💮
💥° 
💨
🌻
😍
😊nếu bạn quý )
🍭
🍬
😉。
🍻
🍸。
🎶 
😚
MK
4
5 tháng 9
20:
a: \(4^{n}=256\)
=>\(4^{n}=4^4\)
=>n=4
b: \(9^{5n-8}=81\)
=>\(9^{5n-8}=9^2\)
=>5n-8=2
=>5n=10
=>n=2
c: \(3^{n+2}:27=3\)
=>\(3^{n+2}=27\cdot3=81=3^4\)
=>n+2=4
=>n=2
d: \(8^{n+2}\cdot2^3=8^5\)
=>\(8^{n+2}=8^5:8=8^4\)
=>n+2=4
=>n=2
Bài 21:
a: \(30-2x^2=12\)
=>\(2x^2=30-12=18\)
=>\(x^2=9\)
mà x>=0(do x là số tự nhiên)
nên x=3
b: \(\left(9-2x\right)^3=125\)
=>9-2x=5
=>2x=4
=>x=2
c: \(\left(2x-2\right)^4=0\)
=>2x-2=0
=>2x=2
=>x=1
d: \(\left(x+5\right)^3=\left(2x\right)^3\)
=>2x=x+5
=>2x-x=5
=>x=5
S
subjects
CTVHS
7 tháng 9
bài 20:
\(a.4^{n}=256\)
\(4^{n}=4^4\)
⇒ n = 4
b . \(9^{5n-8}=81\)
\(9^{5n-8}=9^2\)
⇒ 5n - 8 = 2
5n = 2 + 8
5n = 10
n = 10 : 5 = 2
c. \(3^{n+2}:27=3\)
\(3^{n+2}=3\cdot27\)
\(3^{n+2}=81\)
\(3^{n+2}=3^4\)
⇒ n + 2 = 4
⇒ n = 4 - 2 = 2
d. \(8^{n+2}\cdot2^3=8^5\)
\(8^{n+2}=8^5:2^3\)
\(8^{n+2}=8^4\)
⇒ n + 2 = 4
⇒ n = 4 - 2 = 2
bài 21 :
\(a.30-2x^2=12\)
\(2x^2=30-12\)
\(2x^2=18\)
\(x^2=18:2\)
\(x^2=9\)
⇒ x = 3 hoặc x = -3
b. \(\left(9-2x\right)^3=125\)
\(\left(9-2x\right)^3=5^3\)
⇒ 9 - 2x = 5
2x = 9 - 5
2x = 4
x = 4 : 2 = 2
c. \(\left(2x-2\right)^4=0\)
⇒ 2x - 2 = 0
2x = 2
x = 2 : 2 = 1
d. \(\left(x+5\right)^3=\left(2x\right)^3\)
⇒ x + 5 = 2x
⇒ 2x - x = 5
x = 5
10 tháng 9
a: A={x∈N|x⋮3 và x<=15}
b: B={x∈N|x⋮5 và x<=30}
c: C={x∈N|x⋮10 và x<=90}
d: D={x∈N|x=4k+1; 0<=k<=4}
6 tháng 2 2018
cái này dễ nà!
ta có:
5x + 2 ⋮ x + 1
=> (5x+5) - 5 + 2 ⋮ x + 1
=> (5x+5.1) - 3 ⋮ x + 1
=> 5(x+1) - 3 ⋮ x + 1
có x+1 ⋮ x+1 => 5 (x+1) ⋮ x + 1
=> - 3 ⋮ x + 1
=> x + 1 ∈ Ư(-3)
x ∈ Z => x + 1 ∈ Z
=> x + 1 ∈ {-1;-3;1;3}
=> x ∈ {-2;-4;0;2}
vậy____
KT
6 tháng 2 2018
\(5x+2\)\(⋮\)\(x+1\)
\(\Leftrightarrow\)\(5\left(x+1\right)-3\)\(⋮\)\(x+1\)
Ta thấy \(5\left(x+1\right)\)\(⋮\)\(x+1\)
\(\Leftrightarrow\)\(3\)\(⋮\)\(x+1\)
\(\Rightarrow\)\(x+1\)\(\inƯ\left(3\right)=\left\{\pm1;\pm3\right\}\)
\(\Rightarrow\)\(x=\left\{-4;-2;0;2\right\}\)
16 tháng 8
Bài 5:
a: \(37\cdot146+46\cdot2-46\cdot37\)
\(=37\left(146-46\right)+46\cdot2\)
\(=37\cdot100+92=3700+92=3792\)
b: \(2\cdot5\cdot71+5\cdot18\cdot2+10\cdot11\)
\(=10\cdot71+10\cdot18+10\cdot11\)
\(=10\left(71+18+11\right)=10\cdot100=1000\)
c: \(135+360+65+40\)
=135+65+360+40
=200+400
=600
d: \(27\cdot75+25\cdot27-450\)
\(=27\left(75+25\right)-450\)
=2700-450
=2250
Bài 4:
a: \(32\cdot163+32\cdot837\)
\(=32\cdot\left(163+837\right)\)
\(=32\cdot1000=32000\)
b: \(2\cdot3\cdot4\cdot5\cdot25=2\cdot5\cdot4\cdot25\cdot3=3\cdot10\cdot100=3000\)
c: \(25\cdot27\cdot4=27\cdot100=2700\)
Bài 3:
a: \(128\cdot19+128\cdot41+128\cdot40\)
\(=128\cdot\left(19+41+40\right)=128\cdot100=12800\)
b: \(375+693+625+307\)
=375+625+693+307
=1000+1000
=2000
c: \(37+42-37+22\)
=37-37+42+22
=0+64
=64
d: \(21\cdot32+21\cdot68\)
\(=21\cdot\left(32+68\right)=21\cdot100=2100\)
Bài 2:
a: \(17\cdot85+15\cdot17-120\)
\(=17\left(85+15\right)-120\)
=1700-120
=1580
b: \(189+73+211+127\)
=189+211+73+127
=400+200
=600
c: \(38\cdot73+27\cdot38\)
\(=38\left(73+27\right)=38\cdot100=3800\)
Bài 1:
a: \(28\cdot76+23\cdot28-28\cdot13\)
\(=28\left(76+23-13\right)=28\cdot86=2408\)
b: \(39\cdot50+25\cdot39+75\cdot61\)
\(=39\left(50+25\right)+75\cdot61\)
\(=39\cdot75+75\cdot61=75\left(39+61\right)=75\cdot100=7500\)
c: \(32\cdot163+837\cdot32\)
\(=32\left(163+837\right)=32\cdot1000=32000\)
d: \(63+118+37+82\)
=63+37+118+82
=100+200
=300
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
22 tháng 8
Câu c:
C = \(9^{2n+1}\) + 1
CM C ⋮ 10
Giải:
9 ≡ -1 (mod 10)
\(9^{2n+1}\) ≡ -1\(^{2n+1}\) (mod 10)
9\(^{2n+1}\) ≡ -1 (mod 10)
1 ≡ 1 (mod 10)
Cộng vế với vế ta có:
9\(^{2n+1}\) + 1 ≡ (-1) + 1 (mod 10)
9\(^{2n+1}\) + 1 ≡ 0 (mod 10)
C = 9\(^{2n+1}\) + 1 ⋮ 10 (đpcm)
22 tháng 8
\(n^2+n=n\left(n+1\right)\) là tích của hai số tự nhiên liên tiếp
=>\(n^2+n\) chỉ có thể có tận cùng là 0;2;6
=>\(n^2+n+1\) sẽ có tận cùng là 1;3;7
mà \(1995^{2000}\) có chữ số tận cùng là 5
nên \(n^2+n+1\) sẽ không chia hết cho \(1995^{2000}\)
S
subjects
CTVHS
22 tháng 8
bài 14:
\(a.\left(x-1\right)\cdot100=0\)
\(x-1=0\Rightarrow x=1\)
\(b.200-11x=24\)
\(11x=200-24\)
\(11x=176\)
\(x=\frac{176}{11}=16\)
\(c.165:\left(2x+1\right)=15\) (đkxđ: x khác \(-\frac12)\)
\(2x+1=\frac{165}{15}=11\)
\(2x=11-1=10\)
\(x=\frac{10}{2}=5\)
\(d.375:\left(45-4x\right)=15\) (đkxđ: \(x\ne\frac{45}{4})\)
\(45-4x=\frac{375}{15}=25\)
\(4x=45-25=20\)
\(x=20:4=5\)
bài 15:
giá tiền 125 chiếc điện thoại là:
125 x 2350000=293750000 (đồng)
giá tiền 250 chiếc máy tính bảng là:
250 x 4950000 = 1237500000 (đồng)
tổng số tiền mà cửa hàng phải trả cho số điện thoại và máy tính trên là:
293750000 + 1237500000 = 1531250000 (đồng)
đáp số: 1531250000 đồng
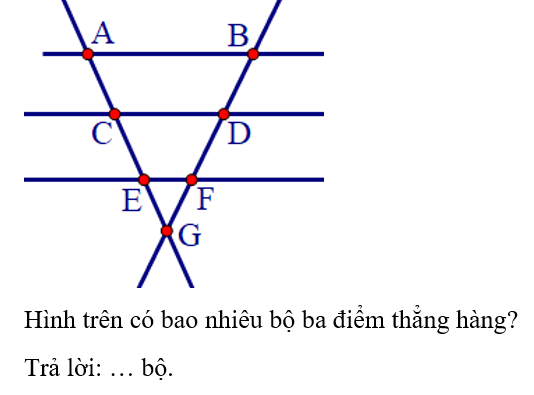
Các bộ ba điểm thẳng hàng trong hình trên lần lượt là:
(A; C; E); (A; C; G); (A; E; G); (C:E;G); (B: D; F;); (B; D; G); (B; F; G); (D; F; G)
Vậy có tất cả 8 bộ ba điểm thẳng hàng.
Cách hai:
Ta có: Do 4 điểm A; C; E; G thẳng hàng nên:
Cứ 3 điểm thẳng hàng thì tạo thành một bộ ba điểm thẳng hàng.
Vậy có 4 cách chọn điểm thứ nhất, 3 cách chọn điểm thứ hai, 2 cách chọn điểm thứ ba. Số bộ ba điểm thẳng hàng là:
4 x 3 x 2 = 24 (bộ)
Theo cách tính trên mỗi bộ được tính 6 lần vậy thực tế số bộ ba điểm thẳng hàng là: 24 : 6 = 4 (bộ)
Chứng minh tương tự xét 4 điểm thằng hàng: B; D; F; G ta có số bộ ba điểm thẳng hàng là: 4 bộ
Tất cả số bộ ba điểm thẳng hàng là:
4 + 4 = 8 (bộ)
Kết luận: Tất cả có 8 bộ ba điểm thẳng hàng.